题目内容
1.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )| A. | 增加6m2 | B. | 减少6m2 | C. | 增加9m2 | D. | 减少9m2 |
分析 设原来的正方形边长为a米,求出正方形的面积与长方形的面积作差即可.
解答 解:设原来的正方形边长为a米,则原来的面积为a2平方米,
改造后的长方形草坪面积为(a+3)(a-3)=a2-9(平方米),
改造后的长方形草坪面积与原来正方形草坪面积相比a2-9-a2=-9(m2),
所以改造后的长方形草坪面积比原来正方形草坪面积减小了9m2.
故选:D.
点评 本题主要考查了平方差公式的几何背景,解题的关键是正确求出正方形与长方形的面积.

练习册系列答案
相关题目
11.在下列实数$\frac{22}{7}$,3.14159265,$\sqrt{8}$,-8,$\root{3}{9}$,$\sqrt{36}$,1.103 030 030 003…(两个3之间依次多一个0),$\frac{π}{3}$中,无理数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
12.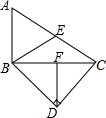 如图,在四边形ABDC中,∠BDC=90°,AB⊥BC,E、F分别是AC、BC的中点,BE、DF的大小关系是( )
如图,在四边形ABDC中,∠BDC=90°,AB⊥BC,E、F分别是AC、BC的中点,BE、DF的大小关系是( )
 如图,在四边形ABDC中,∠BDC=90°,AB⊥BC,E、F分别是AC、BC的中点,BE、DF的大小关系是( )
如图,在四边形ABDC中,∠BDC=90°,AB⊥BC,E、F分别是AC、BC的中点,BE、DF的大小关系是( )| A. | BE>DF | B. | BE=DF | C. | BE<DF | D. | 无法确定 |
6.x与$\frac{2}{3}$的差的一半是正数,用不等式表示为( )
| A. | $\frac{1}{2}$(x-$\frac{2}{3}$)>0 | B. | $\frac{1}{2}$x-$\frac{2}{3}$<0 | C. | $\frac{1}{2}$x-$\frac{2}{3}$>0 | D. | $\frac{1}{2}$(x-$\frac{2}{3}$)<0 |
10.⊙O过点B,C,圆心O在等腰直角△ABC内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
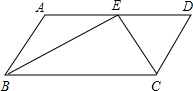 已知:如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=15cm,CE=8cm,求?ABCD的周长和面积.
已知:如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=15cm,CE=8cm,求?ABCD的周长和面积. 如图,在四边形ABCD中,AD∥BC,∠BAD=∠BCD.
如图,在四边形ABCD中,AD∥BC,∠BAD=∠BCD. ,那么
,那么 =_______。
=_______。