题目内容
10.⊙O过点B,C,圆心O在等腰直角△ABC内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
分析 根据等腰三角形三线合一的性质知:若过A作BC的垂线,设垂足为D,则AD必垂直平分BC;由垂径定理可知,AD必过圆心O;根据等腰直角三角形的性质,易求出BD、AD的长,进而可求出OD的值;连接OB根据勾股定理即可求出⊙O的半径.
解答 解:过A作AD⊥BC,由题意可知AD必过点O,连接OB;
∵△BAC是等腰直角三角形,AD⊥BC,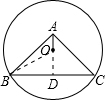
∴BD=CD=AD=3;
∴OD=AD-OA=2;
Rt△OBD中,根据勾股定理,得:
OB=$\sqrt{B{D}^{2}+O{D}^{2}}$=$\sqrt{13}$.
故选C.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
20.为充分利用雨水资源,幸福村的小明家和相邻的爷爷家采取了修建蓄水池、屋顶收集雨水的做法.已知小明和爷爷家的屋顶收集雨水的面积、蓄水池的容积和蓄水池已有水的量如表:
气象预报即将会下雨,为了收集尽可能多的雨水,下雨前需从爷爷家的蓄水池中抽取多少立方米的水注入小明家的蓄水池?
| 小明家 | 爷爷家 | |
| 屋顶收集雨水面积(m2) | 160 | 120 |
| 蓄水池容积(m3) | 50 | 13 |
| 蓄水池已有水量(m3) | 34 | 11.5 |
1.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
| A. | 增加6m2 | B. | 减少6m2 | C. | 增加9m2 | D. | 减少9m2 |
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.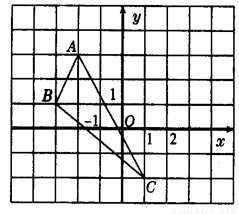
 ,
,  )在第二象限,则k的取值范围是( )
)在第二象限,则k的取值范围是( ) <
<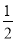 B.
B. 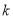 <2 C.
<2 C. 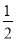 <
<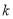 <2 D.
<2 D. 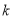 >2
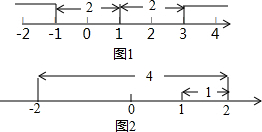
>2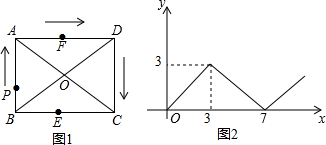 如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )