题目内容
7. 如图,在菱形ABCD中,∠B=120°,AB=4,点E是BC的中点,点F在CD边上,点C关于EF的对称点为C′,连接EC′,FC′,当点F从C运动到点D的过程中,AC′长度的最大值与最小值的差为4$\sqrt{3}$-2$\sqrt{7}$+2.
如图,在菱形ABCD中,∠B=120°,AB=4,点E是BC的中点,点F在CD边上,点C关于EF的对称点为C′,连接EC′,FC′,当点F从C运动到点D的过程中,AC′长度的最大值与最小值的差为4$\sqrt{3}$-2$\sqrt{7}$+2.
分析 先确定最大值:①当F与C重合时,C′与C重合,AC′=AC最大,作对角线求AC即可;
②如图2因为C与C′关于EF对称,所以当点F从C运动到点D的过程中,C′在以E为圆心,以EC为半径的圆上运动,当点C′在AE上时,AC′最小,构建直角三角形利用勾股定理求AE和C′E的长,根据AC′=AE-C′E=2$\sqrt{7}$-2,最后计算最大值与最小值的差即可.
解答  解:①如图1,当F与C重合时,C′与C重合,AC′=AC最大,
解:①如图1,当F与C重合时,C′与C重合,AC′=AC最大,
连接BD,
∵四边形ABCD是菱形,
∴AC⊥BD,∠ABO=$\frac{1}{2}$∠ABC=$\frac{1}{2}×120°$=60°,
Rt△AOB中,∠BAO=30°,
∴OB=2,
∴AO=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴AC′=AC=4$\sqrt{3}$;
②如图2, 因为C与C′关于EF对称,所以当点F从C运动到点D的过程中,C′在以E为圆心,以EC为半径的圆上运动,
因为C与C′关于EF对称,所以当点F从C运动到点D的过程中,C′在以E为圆心,以EC为半径的圆上运动,
∵AE、C′E的长度为定值,
∴当点C′在AE上时,AC′最小,
过点A作AG⊥BC,交CB的延长线于点G,
∵四边形ABCD是菱形,∠B=120°、AB=4,
∴∠ABG=60°,BG=2,AG=2$\sqrt{3}$,
∴GE=2+1=3,
∴AE=$\sqrt{A{G}^{2}+G{E}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{4}^{2}}$=2$\sqrt{7}$,
则AC′=AE-C′E=2$\sqrt{7}$-2,
∴4$\sqrt{3}$-(2$\sqrt{7}$-2)=4$\sqrt{3}$-2$\sqrt{7}$+2,
AC′长度的最大值与最小值的差为:4$\sqrt{3}$-2$\sqrt{7}$+2,
故答案为:4$\sqrt{3}$-2$\sqrt{7}$+2.
点评 此题主要考查了菱形的性质、轴对称的性质、勾股定理及直角三角形30°角的性质,确定最大值和最小值时点C′的位置是解题关键.

 阅读快车系列答案
阅读快车系列答案| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )| A. | 10 | B. | 17 | C. | 20 | D. | 21.5 |
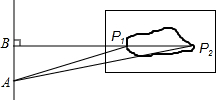 如图是一跳远运动员跳远时落在沙坑的痕迹,则表示该运动员成绩的是( )
如图是一跳远运动员跳远时落在沙坑的痕迹,则表示该运动员成绩的是( )| A. | 线段AP1的长度 | B. | 线段AP2的长度 | C. | 线段BP2的长度 | D. | 线段BP1的长度 |
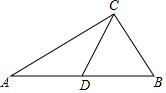 如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )| A. | $\frac{\sqrt{17}-1}{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | $\frac{4}{3}$$\sqrt{3}$ |
 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )| A. | 前2分钟,乙的平均速度比甲快 | |
| B. | 甲、乙两人8分钟各跑了800米 | |
| C. | 5分钟时两人都跑了500米 | |
| D. | 甲跑完800米的平均速度为100米/分 |
