题目内容
16.若矩形的一条对角线长为2,两条对角线的一个交角为60°,则矩形两邻边中较长的一边长为$\sqrt{3}$.分析 依照题意画出图形,由矩形的性质结合∠AOB=60°,即可得出△AOB为等边三角形,即AB=1,再在Rt△ABC中,利用勾股定理求出BC的长度,此题得解.
解答 解:依照题意画出图形,如图所示.
∵四边形ABCD为矩形,且AC=BD=2,
∴AO=BO=1.
∵∠AOB=60°,
∴△AOB为等边三角形,
∴AB=AO=1.
在Rt△ABC中,AB=1,AC=2,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查矩形的性质、等边三角形的判定与性质以及勾股定理,根据矩形的性质结合两条对角线的一个交角为60°,找出矩形两邻边中较短的一边长为1是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.明星队参加“希望杯”篮球比赛,在前8场比赛中的部分积分情况如表:
(1)求本次比赛中,胜一场和负一场各积多少分?
(2)前8场比赛结束时,某队是否存在胜场总积分等于它的负场总积分的情况?为什么?
(3)8场比赛以后还剩余m场比赛,当比赛结束时,该队是否存在胜场总积分等于它的负场总积分的情况?如果存在,求出胜场场次;如果不存在,请说明理由.
| 比赛场次 | 胜场 | 负场 | 积分 |
| m | 0 | m | m |
| 8 | 3 | 5 | 11 |
(2)前8场比赛结束时,某队是否存在胜场总积分等于它的负场总积分的情况?为什么?
(3)8场比赛以后还剩余m场比赛,当比赛结束时,该队是否存在胜场总积分等于它的负场总积分的情况?如果存在,求出胜场场次;如果不存在,请说明理由.
 如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=46°.
如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=46°.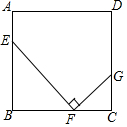 (1)计算:$\frac{x+1}{{{x^2}-1}}$÷$\frac{2}{x-1}$;
(1)计算:$\frac{x+1}{{{x^2}-1}}$÷$\frac{2}{x-1}$;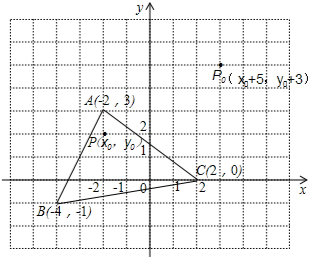 如图,三角形ABC中任意一点P(x0,y0)经平移后对应点P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1.
如图,三角形ABC中任意一点P(x0,y0)经平移后对应点P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1.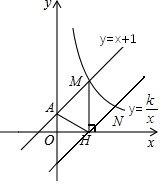 如图,直线y=x+1与y轴交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,MH⊥x轴于点H,tan∠AHO=$\frac{3}{2}$.
如图,直线y=x+1与y轴交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,MH⊥x轴于点H,tan∠AHO=$\frac{3}{2}$.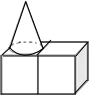 如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,画出实物的三视图.
如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,画出实物的三视图.