题目内容
20. (1)计算:$\frac{x+1}{{{x^2}-1}}$÷$\frac{2}{x-1}$;
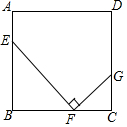
(1)计算:$\frac{x+1}{{{x^2}-1}}$÷$\frac{2}{x-1}$;(2)如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.
分析 (1)先把分母因式分解,再把除法运算化为乘法运算,然后约分即可;
(2)先根据正方形的性质得∠B=∠C=90°,再利用等角的余角相等得∠BEF=∠CFG,然后根据有两组角对应相等的两个三角形相似可判定△EBF∽△FCG.
解答 (1)解:原式=$\frac{x+1}{(x+1)(x-1)}$•$\frac{x-1}{2}$
=$\frac{1}{2}$;
(2)证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,
∴∠BEF+∠BFE=90°,
∵∠EFG=90°,
∴∠BFE+∠CFG=90°,
∴∠BEF=∠CFG,
∴△EBF∽△FCG.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了分式的乘除法和正方形的性质.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
10.下列实数中,为有理数的是( )
| A. | $\sqrt{3}$ | B. | π | C. | $\root{3}{2}$ | D. | 1 |
11.某科普小组有5名成员,身高分别为(单位:cm):160,165,170,163,167.增加1名身高为165cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
| A. | 平均数不变,方差不变 | B. | 平均数不变,方差变大 | ||
| C. | 平均数不变,方差变小 | D. | 平均数变小,方差不变 |
8.若一个三角形的两边长分别为2和4,则该三角形的周长可能是( )
| A. | 6 | B. | 7 | C. | 11 | D. | 12 |
5. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )| A. | $\frac{AD}{AB}=\frac{1}{2}$ | B. | $\frac{AE}{EC}=\frac{1}{2}$ | C. | $\frac{AD}{EC}=\frac{1}{2}$ | D. | $\frac{DE}{BC}=\frac{1}{2}$ |
17.某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如表:
那么这9名学生所得分数的众数和中位数分别是( )
| 人数(人) | 1 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |