题目内容
18. 已知:在梯形ABCD中,AD∥BC,∠AEB=∠ADC.
已知:在梯形ABCD中,AD∥BC,∠AEB=∠ADC.(1)求证:△ADE∽△DBC;
(2)连结EC,若CD2=AD•BC,求证:∠DCE=∠ADB.
分析 (1)由平行线的性质得出∠ADE=∠DBC,∠ADC+∠C=180°,再由已知条件和邻补角关系得出∠AED=∠C,即可得出△ADE∽△DBC;
(2)由(1)得:△ADE∽△DBC,由相似三角形的对应边成比例得出DB•DE=AD•BC,再由已知条件得出$\frac{CD}{DE}=\frac{DB}{CD}$,由公共角相等得出△CDE∽△BDC,得出∠DCE=∠DBC,即可得出结论.
解答 (1)证明:∵AD∥BC,
∴∠ADE=∠DBC,∠ADC+∠C=180°,
∵∠AEB=∠ADC,∠AEB+∠AED=180°,
∴∠AED=∠C,
∴△ADE∽△DBC;
(2)证明:连接EC,如图所示:
由(1)得:△ADE∽△DBC,
∴$\frac{AD}{DB}=\frac{DE}{BC}$,
∴DB•DE=AD•BC,
∵CD2=AD•BC,
∴CD2=DB•DE,
∴$\frac{CD}{DE}=\frac{DB}{CD}$,
又∵∠CDE=∠BDC,
∴△CDE∽△BDC,
∴∠DCE=∠DBC,
又∵∠ADB=∠DBC,
∴∠DCE=∠ADB.
点评 本题考查了相似三角形的判定与性质、平行线的性质、邻补角关系;本题综合性强,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
7.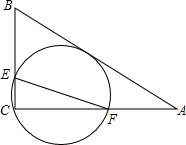 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF的长度( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF的长度( )
 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF的长度( )
如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF的长度( )| A. | 随圆的大小变化而变化,但没有最值 | |
| B. | 最大值为4.8 | |
| C. | 有最小值 | |
| D. | 为定值 |
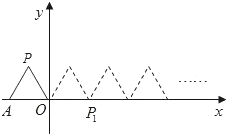 如图,将边长为1的正△OAP沿x轴正方向连续翻转,△OAP第1次翻转后记为△O1A1P1,第2次翻转后记为△O2A2P2,…,如果经过若干次翻转后点P的横坐标是2014,则翻转次数为2014或2015.
如图,将边长为1的正△OAP沿x轴正方向连续翻转,△OAP第1次翻转后记为△O1A1P1,第2次翻转后记为△O2A2P2,…,如果经过若干次翻转后点P的横坐标是2014,则翻转次数为2014或2015. 如图,O是线段AB的中点,C在直线AB上,AC=4,CB=3,则OC的长等于0.5.
如图,O是线段AB的中点,C在直线AB上,AC=4,CB=3,则OC的长等于0.5. 如图,D、E在BC上,AB=AC且,AD=AE,求证:BD=CE.
如图,D、E在BC上,AB=AC且,AD=AE,求证:BD=CE. 一辆快车从甲地开始,一辆慢车从乙地开始都往返于甲乙两地之间,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线A-B-C-D-E表示:从两车出发后一部分y与x之间的函数关系.
一辆快车从甲地开始,一辆慢车从乙地开始都往返于甲乙两地之间,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线A-B-C-D-E表示:从两车出发后一部分y与x之间的函数关系. 如图,点C是线段AB上一点,AC<CB,M、N分别是AB和CB的中点,AC=8,NB=5,则线段MN=4.
如图,点C是线段AB上一点,AC<CB,M、N分别是AB和CB的中点,AC=8,NB=5,则线段MN=4.