题目内容
7．
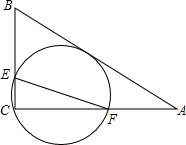如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F，则线段EF的长度（ ）| A． | 随圆的大小变化而变化，但没有最值 | |
| B． | 最大值为4.8 | |
| C． | 有最小值 | |
| D． | 为定值 |
分析 利用勾股定理的逆定理，由三角形的三边长可得△ABC为Rt△，根据90°的圆周角所对的弦为直径得出EF为圆的直径，又圆与AB相切，设切点为D，可知当CD⊥AB时，根据点到直线的垂线段最短可得CD最短，此时EF亦最小．
解答 
解：由题意得，AB2=AC2+BC2，
∴△ABC为RT△，即∠C=90°，可知EF为圆的直径，
设圆与AB的切点为D，连接CD，
当CD⊥AB，即CD是圆的直径的时候，EF长度最小．
故选C．
点评 此题考查了圆周角定理，勾股定理的逆定理，垂线段最短以及切线的性质，解题的关键是根据题意得出EF为圆的直径，故当CD是直径时EF最小．
练习册系列答案
相关题目
17．若二次函数y=x2-4x+k的图象经过点（-1，y1），（3，y2），则y1与y2的大小关系为（ ）
| A． | y1＞y2 | B． | y1=y2 | C． | y1＜y2 | D． | 不能确定 |
已知：在梯形ABCD中，AD∥BC，∠AEB=∠ADC．
如图，C为线段AB的中点，D在线CB上，DA=6，DB=4，求：
2．不透明的袋中装有大小，质地都相同的3个白球和6个黄球，从中随机摸出一个，则摸到黄球的概率为（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{5}$ |
如图，BC是⊙O的直径，P是CB延长线上一点，PA切⊙O于点A，如果PA=4，PB=2，那么线段BC的长等于（ ）