题目内容
17.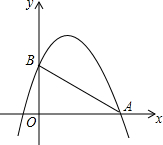 如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3).
如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3).(1)求此抛物线所对应的函数关系式;
(2)在x轴的正半轴上是否存在点M.使得AM=BM?若存在,求出点M的坐标;若不存在,请说明理由.
分析 (1)用待定系数直接求之即可;
(2)作AB的垂直平分线交x轴于点M,利用勾股定理算出OM即可.
解答 解:(1)把点A(4,0),B(0,3)代入二次函数y=-x2+bx+c得
$\left\{\begin{array}{l}{-16+4b+c=0}\\{c=3}\end{array}\right.$,
解得:$b=\frac{13}{4}$,c=3,
所以二次函数的关系式为:$y=-{x}^{2}+\frac{13}{4}x+3$;
(2)如图,作AB的垂直平分线交x轴于点M,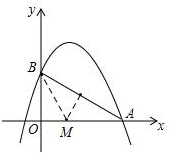
连接BM,则BM=AM,
设BM=AM=x,
则OM=4-x,
在直角△OBM中,
BM2=OB2+OM2,
即:x2=32+(4-x)2,
解得:x=$\frac{25}{8}$,
∴OM=4-$\frac{25}{8}$=$\frac{7}{8}$,
所以点M的坐标为:($\frac{7}{8}$,0);
点评 本题考查了待定系数求二次函数解析式、垂直平分线的性质、勾股定理等知识点,难度不大,属于基础题.第(2)问虽然简单,却是对称问题与勾股定理相结合的经典应用,要引起重视.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
1.某下岗职工购进一批香蕉,到集贸市场零售.已知卖出的香蕉数量x与销售额y的关系如表所示:
求y与x的函数关系式,并指出y是不是x的一次函数.
| 数量x(千克) | 1 | 2 | 3 | 4 | 5 |
| 销售额y(元) | 4+0.1 | 8+0.2 | 12+0.3 | 16+0.4 | 20+0.5 |
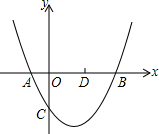 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).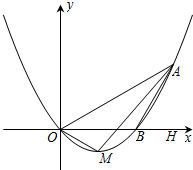 如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AB=BO=2,∠AOB=30°.
如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AB=BO=2,∠AOB=30°.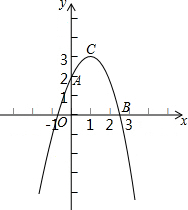 已知点B(2,0),抛物线y=-x2+2x+2与y轴交于点A.
已知点B(2,0),抛物线y=-x2+2x+2与y轴交于点A.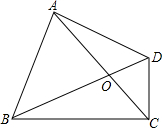 四边形ABCD中,AC、BD相交于点O,∠BAD=90°且AB=AD,CD⊥BC,∠ACB=45°,AC=BC.
四边形ABCD中,AC、BD相交于点O,∠BAD=90°且AB=AD,CD⊥BC,∠ACB=45°,AC=BC.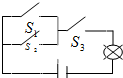 如图,随机闭合开关中的两个,能够让灯泡发光的概率为$\frac{2}{3}$.
如图,随机闭合开关中的两个,能够让灯泡发光的概率为$\frac{2}{3}$.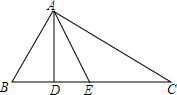 已知:如图所示,△ABC中,AD⊥BC,AB=AE,点E在AC的垂直平分线上.
已知:如图所示,△ABC中,AD⊥BC,AB=AE,点E在AC的垂直平分线上.