题目内容
2.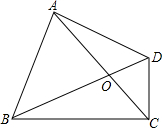 四边形ABCD中,AC、BD相交于点O,∠BAD=90°且AB=AD,CD⊥BC,∠ACB=45°,AC=BC.
四边形ABCD中,AC、BD相交于点O,∠BAD=90°且AB=AD,CD⊥BC,∠ACB=45°,AC=BC.(1)求证:△DCA≌△OCB;
(2)若AC=4,求出四边形ABCD的面积.
分析 (1)由∠BAD=90°,CD⊥BC,得到A,B,C,D四点共圆,根据圆周角定理得到∠DAO=∠CAO,∠ACD=∠ACB,即可得到结论;
(2)过B作BE⊥AC于E,过D作DF⊥AC于F,由∠ECB=∠DCF=45°,于是得到BE=CE,DF=CF,根据余角的性质得到∠ABE=∠DAE,推出△ABE≌△ADF,根据全等三角形的性质得到AF=BE,AE=DF,等量代换得到AE=CF,求得BE+DF=AF+CF=AC=4,即可得到结论.
解答 (1)证明:∵∠BAD=90°,CD⊥BC,
∴A,B,C,D四点共圆,
∴∠DAO=∠CAO,
∵AB=AD,
∴$\widehat{AB}=\widehat{AD}$,
∴∠ACD=∠ACB,
在△DCA与△OCB中,
$\left\{\begin{array}{l}{∠DAC=∠OBC}\\{∠ACD=∠BCO}\\{AC=BC}\end{array}\right.$,
∴△DCA≌△OCB;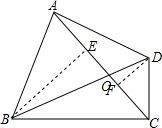
(2)解:过B作BE⊥AC于E,过D作DF⊥AC于F,
∵∠ECB=∠DCF=45°,
∴BE=CE,DF=CF,
∵∠BAE+∠DAE=∠BAE+∠ABE=90°,
∴∠ABE=∠DAE,
在△ABE与△ADF中,
$\left\{\begin{array}{l}{∠AEB=∠AFD=90°}\\{∠ABE=∠DAF}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADF,
∴AF=BE,AE=DF,
∴AE=CF,
∴BE+DF=AF+CF=AC=4,
∴S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$AC$•BE+\frac{1}{2}AC•DF$,
∴S四边形ABCD=$\frac{1}{2}$AC2=8.
点评 本题考查了全等三角形的判定和性质,四点共圆,求图形的面积,正确的作出辅助线是解题的关键.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案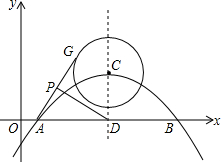 已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )
已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{{\sqrt{41}}}{2}$ | C. | $\frac{{\sqrt{34}}}{2}$ | D. | $2\sqrt{3}$ |
①2、3、4 ②3、4、5 ③15、20、25 ④7、24、25.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | -2,4 | B. | 2,3 | C. | -2,3 | D. | 2,4 |
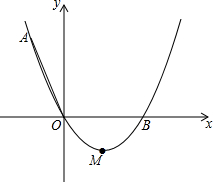 如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=4,∠AOB=120°.
如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=4,∠AOB=120°.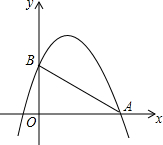 如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3).
如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3). 如图,C是线段AB上一点,M为AB的中点,N为AC的中点,若AB=20cm,AC=14cm,则MN=3cm.
如图,C是线段AB上一点,M为AB的中点,N为AC的中点,若AB=20cm,AC=14cm,则MN=3cm.