题目内容
7.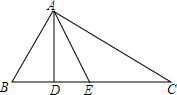 已知:如图所示,△ABC中,AD⊥BC,AB=AE,点E在AC的垂直平分线上.
已知:如图所示,△ABC中,AD⊥BC,AB=AE,点E在AC的垂直平分线上.(1)请问:AB、BD、DC有何数量关系?并说明理由;
(2)如果CD=3BD,求∠B的度数.
分析 (1)由△ABC中,AD⊥BC,AB=AE,根据三线合一的性质,可得BD=DE,又由点E在AC的垂直平分线上,根据线段垂直平分线的性质,可得AE=CE,继而证得DC=AB+BD;
(2)由CD=3BD,结合(1)中的结论,易证得AB=2BD,继而求得∠BAD=30°,则可求得∠B的度数.
解答 解:(1)AB+BD=DC.
理由:∵△ABC中,AD⊥BC,AB=AE,
∴BD=DE,
∵点E在AC的垂直平分线上,
∴AE=CE,
∴CE=AB,
∴AB+BD=CE+DE=DC.
(2)∵CD=3BD,AB+BD=CD,
∴AB=2BD,
∵AD⊥BC,
∴∠BAD=30°,
∴∠B=90°-∠BAD=60°.
点评 此题考查了线段垂直平分线的性质、等腰三角形的性质以及含30°角的直角三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
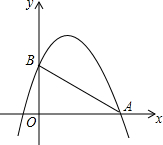 如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3).
如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3). 如图,C是线段AB上一点,M为AB的中点,N为AC的中点,若AB=20cm,AC=14cm,则MN=3cm.
如图,C是线段AB上一点,M为AB的中点,N为AC的中点,若AB=20cm,AC=14cm,则MN=3cm. 如图,若O为△ABC的两条中线AD和BE的交点,则S△BOD:S△BEC=1:3.
如图,若O为△ABC的两条中线AD和BE的交点,则S△BOD:S△BEC=1:3.