题目内容
12.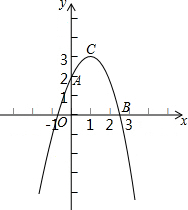 已知点B(2,0),抛物线y=-x2+2x+2与y轴交于点A.
已知点B(2,0),抛物线y=-x2+2x+2与y轴交于点A.(1)此抛物线的顶点坐标C(1,3);
(2)若代数式-x2+2x+2的值为大于1的正整数,则x的值为0、1、2;
(3)在抛物线上是否存在点P,使得以AB为直角边的△ABP为直角三角形?如果存在,请求出符合条件的所有点P坐标;如不存在,请说明理由.
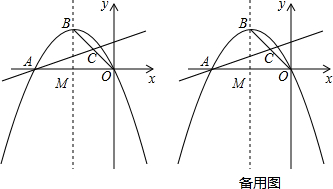
(4)连接AB,D为线段AB上任意一点(不与A、B重合),经过A、D、O三点的圆交直线AC于点E,当△OED的面积取得最小值时,求点D的坐标.
分析 (1)将解析式写成顶点式即可;
(2)分别让y取2和3,解出x即可;
(3)分别作AP⊥AB、BP⊥AB,再分别让AP、BP的解析式与抛物线解析式联立即可解出相应的P点;
(3)由于AD⊥AE,加上AEOD四点共圆,可知∠EOD=90°,另外,∠OAB=45°,于是得出△OED是等腰直角三角形,所以只需让OD最小即可,而当D为AB中点时最小.
解答 解:(1)∵y=-x2+2x+2=-(x-1)2+3,
∴C(1,3);
(2)∵1<y≤3,y为正整数,
∴y=2或3,
令-x2+2x+2=0,解得:x=0或x=2;
令-x2+2x+2=3,解得:x=1;
∴x的值为0、1、2;
(3)令x=0,得y=2,
∴A(0,2),
∵B(2,0),
∴直线AB的解析式为:y=-x+2;
①作点A作AP⊥AB交抛物线于另一点P,如图1,
则直线AP的解析式为:y=x+2,
由$\left\{\begin{array}{l}{y=x+2}\\{y=-{x}^{2}+2x+2}\end{array}\right.$解得:$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$(舍去);
∴P(1,3),即与C点重合;
②过点B作BP⊥AB交抛物线于点P,如图2,
则PB的解析式为:y=x-2,
由$\left\{\begin{array}{l}{y=x-2}\\{y=-{x}^{2}+2x+2}\end{array}\right.$解得:$\left\{\begin{array}{l}{x=\frac{1+\sqrt{17}}{2}}\\{y=\frac{\sqrt{17}-4}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1-\sqrt{17}}{2}}\\{y=\frac{-3-\sqrt{17}}{2}}\end{array}\right.$,
∴P($\frac{1+\sqrt{17}}{2}$,$\frac{\sqrt{17}-4}{2}$)或P($\frac{1-\sqrt{17}}{2}$,$\frac{-3-\sqrt{17}}{2}$)
综上所述,满足要求的P点坐标为:(1,3)、($\frac{1+\sqrt{17}}{2}$,$\frac{\sqrt{17}-4}{2}$)、($\frac{1-\sqrt{17}}{2}$,$\frac{-3-\sqrt{17}}{2}$);
(4)如图3,
由(3)可知,AB⊥AC,
∴∠EAB=90°,
∵A、E、O、D四点共圆,
∴EO⊥OD,
∵AO=BO=2,
∴∠OAB=45°,
∴∠OED=45°,
∴OE=OD,
∴当OD最小时,△OED的面积最小,
根据垂线段最短可知,当OD⊥AB时,OD最小,此时,D为AB的中点,
∴D(1,1).
点评 本题考查了抛物线的顶点式、解一元二次方程、直角三角形的判定与性质、相互垂直的两直线的性质、等腰直角三角形的性质、四点共圆的性质、垂线段最短原理,中点坐标公式等知识点,综合性强,难度较大.第(3)问注意分类讨论,不要漏解;第(4)问的关键是证明三角形OED是等腰直角三角形.

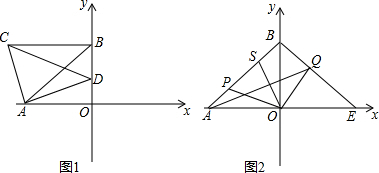
 如图,小球起始位置为(1,0),沿图所示的方向撞击小球,小球首先到达(0,1)处,小球撞到x轴,y轴,直线x=8和直线y=4时都会发生反弹.请你运用所学的知识,画出小球的运动轨迹,并说明小球能否回到起始位置(1,0)处.
如图,小球起始位置为(1,0),沿图所示的方向撞击小球,小球首先到达(0,1)处,小球撞到x轴,y轴,直线x=8和直线y=4时都会发生反弹.请你运用所学的知识,画出小球的运动轨迹,并说明小球能否回到起始位置(1,0)处.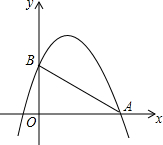 如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3).
如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3).