题目内容
5.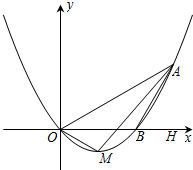 如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AB=BO=2,∠AOB=30°.
如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AB=BO=2,∠AOB=30°.(1)求这条抛物线的表达式;
(2)连结OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.
分析 (1)求出A、B两点坐标,用待定系数法求之即可;
(2)由∠AOB=30°,所以只需求出∠BOM即可,也就只需求∠BOM的正切即可;
(3)分两种情况讨论:①$\frac{BA}{BC}=\frac{OA}{OM}$;②$\frac{BC}{BA}=\frac{OA}{OM}$.
解答 解:(1)如图1,过点A作AH⊥x轴,垂足为H.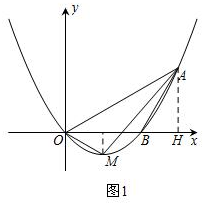
∵AB=BO,
∴∠∠OAB=∠AOB=30°,
∴∠ABH=60°,
在Rt△ABH中,AB=2,
∴BH=1,AH=$\sqrt{3}$,
∴A(3,$\sqrt{3}$),
∵抛物线与x轴交于O、B(2,0)两点,
设y=ax(x-2),代入点A(3,$\sqrt{3}$),可得a=$\frac{\sqrt{3}}{3}$,
∴抛物线的表达式为$y=\frac{\sqrt{3}}{3}x(x-2)$=$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2\sqrt{3}}{3}x$;
(2)由$y=\frac{\sqrt{3}}{3}{x}^{2}-\frac{2\sqrt{3}}{3}x=\frac{\sqrt{3}}{3}(x-1)^{2}-\frac{\sqrt{3}}{3}$,
得抛物线的顶点M的坐标为(1,-$\frac{\sqrt{3}}{3}$),
∴$tan∠BOM=\frac{\sqrt{3}}{3}$,
∴∠BOM=30°,
∴∠AOM=60°;
(3)由A(3,$\sqrt{3}$),、B(2,0)、M(1,-$\frac{\sqrt{3}}{3}$),
∵AH⊥x轴,∠AOB=30°,
∴AO=2AH=$2\sqrt{3}$,
∵M(1,-$\frac{\sqrt{3}}{3}$),∠BOM=30°,
∴$OM=\frac{2\sqrt{3}}{3}$,
∴$\frac{OA}{OM}=3$,
当点C在点B左侧时,∠ABC=120°,△AMO中不可能出现120°的角,不存在满足条件的点;
当点C在点B右侧时,∵∠ABC=∠AOM=60°,
∴△ABC与△AOM相似,存在两种情况:
①如图2,当$\frac{BA}{BC}=\frac{OA}{OM}=3$时,$BC=\frac{1}{3}BA=\frac{2}{3}$.此时C($\frac{8}{3}$,0);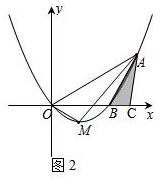
②如图3,当$\frac{BC}{BA}=\frac{OA}{OM}=3$时,BC=3BA=3×2=6.此时C(8,0).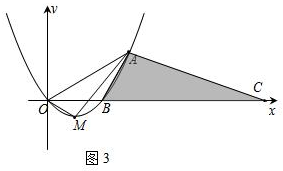
综上所述,C点的坐标为($\frac{8}{3}$,0)或(8,0).
点评 本题考查了待定系数法求二次函数解析式、特殊角的三角函数、解直角三角形、相似三角形的判定与性质等知识点,有一定综合性,难度适中.第(3)问注意分类讨论.分类讨论之前,可先通过分析排除不存在的情况,使解答过程得以简化.

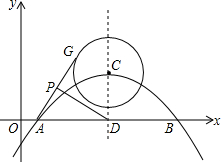 已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )
已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{{\sqrt{41}}}{2}$ | C. | $\frac{{\sqrt{34}}}{2}$ | D. | $2\sqrt{3}$ |
①2、3、4 ②3、4、5 ③15、20、25 ④7、24、25.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
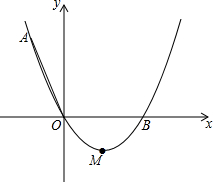 如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=4,∠AOB=120°.
如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=4,∠AOB=120°.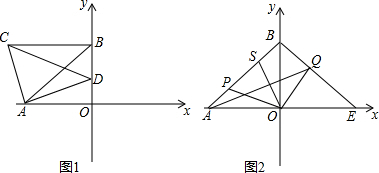
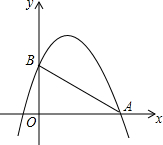 如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3).
如图所示,已知抛物线y=-x2+bx+c与x轴的一个交点为A(4,0),与y轴交于点B(0,3).