题目内容
17. 在△ABC中,∠ACB=90°,AC=BC,AB=10,用尺规作图的方法作线段AD和线段DE,保留作图痕迹如图所示,认真观察作图痕迹,则△BDE的周长是( )
在△ABC中,∠ACB=90°,AC=BC,AB=10,用尺规作图的方法作线段AD和线段DE,保留作图痕迹如图所示,认真观察作图痕迹,则△BDE的周长是( )| A. | 8 | B. | 5$\sqrt{2}$ | C. | $\frac{15}{2}$$\sqrt{2}$ | D. | 10 |
分析 根据等腰直角三角形的性质得到∠B=45°,根据尺规作图可知AD平分∠CAB,根据角平分线的性质定理解答即可.
解答 解:∵∠ACB=90°,AC=BC,
∴∠B=45°,
由尺规作图可知,AD平分∠CAB,DE⊥AB又,∠ACB=90°,
∴DE=DC,又∠B=45°,
∴DE=BE,
∴△BDE的周长=BD+BE+DE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB=10,
故选:D.
点评 本题考查的是等腰直角三角形的性质以及尺规作图,掌握等腰直角三角形的性质和基本尺规作图是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.抛物线y=ax2+bx+c的图象只经过第一、二象限,那么关于△=b2-4ac,下列结论成立的是( )
| A. | △<0 | B. | △≤0 | C. | △>0 | D. | △≥0 |
 向某一容器中注水,注满为止,表示注水量与水深的函数关系的图象大致如图所示,则该容器可能是( )
向某一容器中注水,注满为止,表示注水量与水深的函数关系的图象大致如图所示,则该容器可能是( )



 如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,若S△ABD=10cm2,S△ACD为( )
如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,若S△ABD=10cm2,S△ACD为( )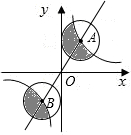 如图,正比例函数y=2x的图象和反比例函数$y=\frac{8}{x}$的图象相交于A、B两点,以A、B为圆心的两圆均与y轴相切,则图中阴影部分的面积之和等于( )
如图,正比例函数y=2x的图象和反比例函数$y=\frac{8}{x}$的图象相交于A、B两点,以A、B为圆心的两圆均与y轴相切,则图中阴影部分的面积之和等于( ) 画出如图所示几何体的主视图和左视图.
画出如图所示几何体的主视图和左视图.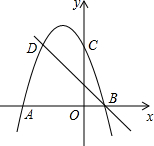 如图,二次函数的图象与x轴交于点A(-3,0),B(1,0),交y轴于点C(0,3),点C,D是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点B,D.
如图,二次函数的图象与x轴交于点A(-3,0),B(1,0),交y轴于点C(0,3),点C,D是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点B,D.