题目内容
5.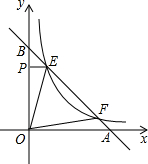 如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2.
如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2.(1)求反比例函数的解析式;
(2)如果直线EF的解析式是y=-x+n,计算△OEF的面积.
分析 (1)作EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,根据反比例函数的比例系数的几何意义由△OEP的面积为2易得k=4.
(2)求得反比例函数解析式为y=$\frac{4}{x}$,再证明△BPE∽△BHF,利用相似比可得HF=4PE,根据反比例函数图象上点的坐标特征,设E点坐标为(t,$\frac{4}{t}$),则F点的坐标为(4t,$\frac{4}{4t}$),由于S△OEF+S△OFD=S△OEC+S梯形ECDF,S△OFD=S△OEC=2,所以S△OEF=S梯形ECDF,然后根据梯形面积公式计算.
解答 解:(1)作EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,如图,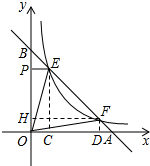
∵△OEP的面积为2,
∴$\frac{1}{2}$|k|=2,
而k>0,
∴k=4,
∴反比例函数解析式为y=$\frac{4}{x}$,
(2)∵EP⊥y轴,FH⊥y轴,
∴EP∥FH,
∴△BPE∽△BHF,
∴$\frac{PE}{HF}$=$\frac{BE}{BF}$=$\frac{1}{4}$,即HF=4PE,
设E点坐标为(t,$\frac{4}{t}$),则F点的坐标为(4t,$\frac{4}{4t}$),
∵S△OEF+S△OFD=S△OEC+S梯形ECDF,
而S△OFD=S△OEC=2,
∴S△OEF=S梯形ECDF=$\frac{1}{2}$($\frac{4}{4t}$+$\frac{4}{t}$)(4t-t)
=$\frac{15}{2}$.
点评 本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、反比例函数的比例系数的几何意义;会利用相似比确定线段之间的关系.

练习册系列答案
相关题目
16.为迎接“六一”儿童节,某儿童品牌玩具专卖店购进了A、B两类玩具,其中A类玩具的进价比B类玩具的进价每个多3元,经调查:用900元购进A类玩具的数量与用750元购进B类玩具的数量相同.设A类玩具的进价为m元/个,根据题意可列分式方程为( )
| A. | $\frac{900}{m}=\frac{750}{m+3}$ | B. | $\frac{900}{m+3}=\frac{750}{m}$ | C. | $\frac{900}{m}=\frac{750}{m-3}$ | D. | $\frac{900}{m-3}=\frac{750}{m}$ |
16.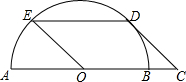 如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
 如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{6}$ | D. | 3$\sqrt{3}$ |
10.下列函数中,y是x的正比例函数的是( )
| A. | y=2x-1 | B. | y=$\frac{3}{x}$ | C. | y=2x | D. | y=$\frac{2}{x}$ |
15.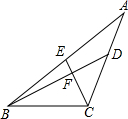 已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
 已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )| A. | $\frac{16}{3}$ | B. | 8 | C. | 4 | D. | 6 |
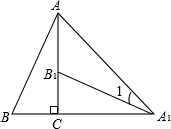 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是60°.
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是60°.
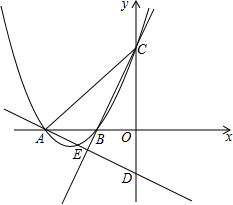 如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,
如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,