题目内容
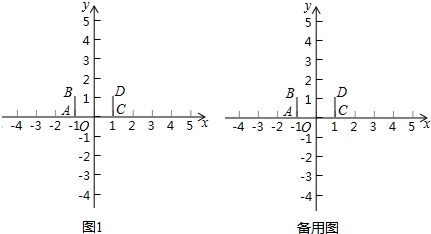
20.如图1,在平面直角坐标系xOy内,已知点A(-1,0),B(-1,1),C(1,0),D(1,1),记线段AB为T1,线段CD为T2,点P是坐标系内一点.给出如下定义:若存在过点P的直线l与T1,T2都有公共点,则称点P是T1-T2联络点.例如,点P$(0,\frac{1}{2})$是T1-T2联络点.(1)以下各点中,②③是T1-T2联络点(填出所有正确的序号);
①(0,2);②(-4,2);③(3,2).
(2)直接在图1中画出所有T1-T2联络点所组成的区域,用阴影部分表示;
(3)已知点M在y轴上,以M为圆心,r为半径画圆,⊙M上只有一个点为T1-T2联络点,
①若r=1,求点M的纵坐标;
②求r的取值范围.
分析 (1)根据题意逐个判断即可;
(2)根据联络点的意义画出图形是直线AD和直线BC围成的区域;
(3)分为两种情况:①⊙M和直线AC相切于(0,0),②与直线BD相切于(0,1),点M在y轴上,⊙M上只有一个点为T1-T2联络点,得出阴影部分关于y轴对称,作ME⊥AD于E,设AD与BC的交点为F,在Rt△AOF中,∠AOF=90°,AO=1,$OF=\frac{1}{2}$,求出AF,在Rt△FEM中,∠FEM=90°,FM=FO+OM=r+$\frac{1}{2}$,$sin∠EFM=sin∠AFO=\frac{{2\sqrt{5}}}{5}$,求出ME,即可求出r的范围.
解答 解:(1)②,③是T1-T2的联络点,
故答案为:②③;
(2)所有T1-T2的联络点所组成的区域为图中阴影部分(含边界),如图所示: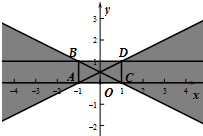 ;
;
(3)①∵点M在y轴上,⊙M上只有一个点为T1-T2的联络点,阴影部分关于y轴对称,
∴⊙M和直线AC相切于(0,0),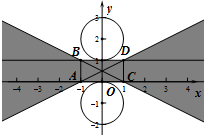 或与直线BD相切于(0,1),如图所示,
或与直线BD相切于(0,1),如图所示,
又∵⊙M的半径r=1,
∴点M的坐标为(0,-1)或(0,2),
经检验:此时⊙M与直线AD,BC无交点,⊙M上只有一个点为T1-T2联络点,符合题意.
∴点M的坐标为(0,-1)或(0,2),
∴点M的纵坐标为-1或2;
②阴影部分关于直线$y=\frac{1}{2}$对称,故不妨设点M位于阴影部分下方.
∵点M在y轴上,⊙M上只有一个点为T1-T2联络点,
阴影部分关于y轴对称,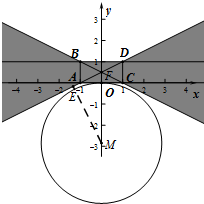
∴⊙M与直线AC相切于O(0,0),且⊙M与直线AD相离.
作ME⊥AD于E,设AD与BC的交点为F,
∴MO=r,ME>r,F(0,$\frac{1}{2}$).
在Rt△AOF中,∠AOF=90°,AO=1,$OF=\frac{1}{2}$,
∴$AF=\sqrt{A{O^2}+O{F^2}}=\frac{{\sqrt{5}}}{2}$,$sin∠AFO=\frac{AO}{AF}=\frac{{2\sqrt{5}}}{5}$,
在Rt△FEM中,∠FEM=90°,FM=FO+OM=r+$\frac{1}{2}$,$sin∠EFM=sin∠AFO=\frac{{2\sqrt{5}}}{5}$,
∴$ME=FM•sin∠EFM=\frac{{\sqrt{5}(2r+1)}}{5}$.
∴$\frac{{\sqrt{5}(2r+1)}}{5}>r$,
又∵r>0,
∴$0<r<\sqrt{5}+2$.
点评 本题考查了直线和圆的位置关系,切线的性质,解直角三角形,轴对称的性质等知识点的应用,能综合运用知识点进行推理和计算是解此题的关键,难度偏大.

| x(元/个) | 30 | 40 | 50 |
| y(个) | 190 | 170 | 150 |
(2)若该商品的销售单价在45元~80元之间浮动.
①销售单价定为多少元时,销售利润最大?此时销售量为多少?
②商店想要在这段时间内获得4550元的销售利润,销售单价应定为多少元?
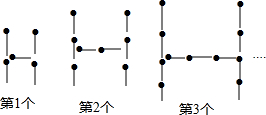
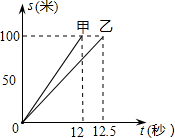 假定甲、乙两人在一次赛跑中,路程S与时间T的关系在平面直角坐标系中所示,如图,请结合图形和数据回答问题:甲到达终点时,乙离终点还有4米.
假定甲、乙两人在一次赛跑中,路程S与时间T的关系在平面直角坐标系中所示,如图,请结合图形和数据回答问题:甲到达终点时,乙离终点还有4米.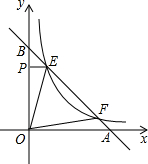 如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2.
如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2. 已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的 交点Q的纵坐标为4.
已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的 交点Q的纵坐标为4.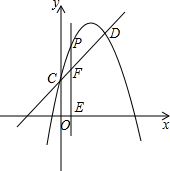 如图,抛物线y=-x2+bx+c与直线y=x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,5).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
如图,抛物线y=-x2+bx+c与直线y=x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,5).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.