题目内容
16.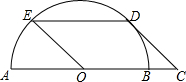 如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{6}$ | D. | 3$\sqrt{3}$ |
分析 连接OD,根据切线的性质得到∠CDO=90°,由四边形OCDE是平行四边形,得到CD=OE,CD∥OE,证得△DOE是等腰直角三角形,于是即可得到结果.
解答  解:连接OD,
解:连接OD,
∴OD=OE,
∵CD与半圆O相切,
∴∠CDO=90°,
∵四边形OCDE是平行四边形,
∴CD=OE,CD∥OE,
∴∠DOE=90°,OD=OE=CD=4,
∴DE=4$\sqrt{2}$.
故选B.
点评 本题考查了切线的性质,平行四边形的性质,等腰直角三角形的性质,连接OD,构造等腰直角三角形是解题的关键.

练习册系列答案
相关题目
7. 如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )
如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )
 如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )
如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )| A. | 12 | B. | 14 | C. | 16 | D. | 无法计算 |
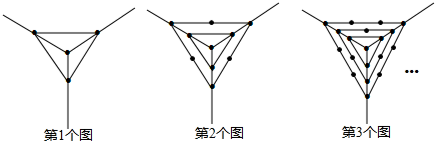
 定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.
定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.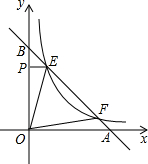 如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2.
如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2.