题目内容
19.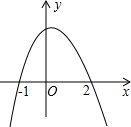 如图是抛物线y=-x2+bx+c的图象,根据图象回答下列问题.
如图是抛物线y=-x2+bx+c的图象,根据图象回答下列问题.(1)求抛物线y=-x2+bx+c的解析式.
(2)方程x2-bx-c=0的解是什么?
(3)当x取什么值时,y>0?
(4)当x取什么值时,y<0?
分析 (1)代入与x轴的交点坐标,建立b、c的二元一次方程组,求得答案即可;
(2)直接观察图象,抛物线与x轴交于-1,2两点,所以方程的解为x1=-1,x2=2;
(3)若y>0,则函数的图象在x轴的上方,找到对应的自变量取值范围即可;
(4)若y<0,则函数的图象在x轴的下方,找到对应的自变量取值范围即可.
解答 解:(1)由图象可知:与x轴的交点坐标为(-1,0),(2,0),
代入y=-x2+bx+c得
$\left\{\begin{array}{l}{-1-b+c=0}\\{-4+2b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=1}\\{c=2}\end{array}\right.$,
抛物线y=-x2+x+2.
(2)观察图象可看对称轴出抛物线与x轴交于x=-1和x=2两点,
方程x2-x-2=0的解为x1=-1,x2=2;
(3)若y>0,则函数的图象在x轴的上方,由函数的图象可知:-1<x<2;
(4)若y<0,则函数的图象在x轴的下方,由函数的图象可知:x>2或x<-1.
点评 本题考查了用待定系数法求函数解析式的方法,体现数形结合的思想解决问题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
9.在一定限度内,每悬挂一定质量的物体,弹簧就会相应拉长一段长度,有一种弹簧的长度(cm)与所悬挂物体的质量(kg)之间的关系如下表所示:
(1)悬挂质量为x(kg)的物体后弹簧的长度为(8+0.6x)cm.
(2)若悬挂物体后弹簧的长度为17cm,求该物体的质量.
| 悬挂物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | … |
| 弹簧的长度(cm) | 8 | 8.6 | 9.2 | 9.8 | 10.4 | … |
(2)若悬挂物体后弹簧的长度为17cm,求该物体的质量.
11.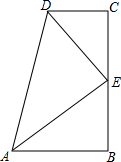 如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
 如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )| A. | E是BC的中点 | B. | CD+AB=AD | C. | ∠AED=90° | D. | CE+DE=BC |
 如图.在△ABC中,BC=AC,CD是∠ACB的平分线.有下列结论:
如图.在△ABC中,BC=AC,CD是∠ACB的平分线.有下列结论: 如图,已知边长为2米的正方形铁架DEFG的正上方有一个灯泡A,测得铁架左右两边的影长分别为BE=6米,CF=4米,试求灯泡距地面的高度.
如图,已知边长为2米的正方形铁架DEFG的正上方有一个灯泡A,测得铁架左右两边的影长分别为BE=6米,CF=4米,试求灯泡距地面的高度.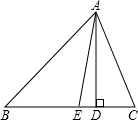 如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.
如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.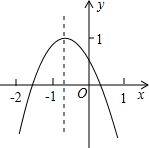 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )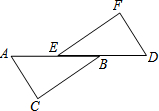 如图,A,E,B,D在同一直线上,在△ABC与△DEF中,AB=DE,AC=DF,AC∥DF.求证:∠C=∠F.
如图,A,E,B,D在同一直线上,在△ABC与△DEF中,AB=DE,AC=DF,AC∥DF.求证:∠C=∠F.