题目内容
4．
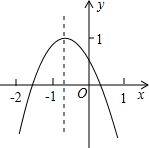二次函数y=ax2+bx+c（a≠0）的图象如图所示，若M=a+b+c，N=a-c，P=-$\frac{b}{2a}$，则在M，N，P中，值小于0的数有（ ）| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
分析 首先根据抛物线的开口方向、对称轴、与y轴交点的坐标可确定出a、b、c的符号，当x=1时，y=M=a+b+c．
解答 解：∵抛物线开口向下，
∴a＜0．
∵抛物线的对称轴位于y轴的左侧，
∴P=-$\frac{b}{2a}$＜0．
∵抛物线与y轴交于正半轴，
∴c＞0．
∴N=a-c＜0．
∵当x=1时，y=a+b+c＜0，
∴M＜0．
故小于0的有3个．
故选：A．
点评 本题主要考查的是二次函数的图象和性质，掌握二次函数的图象和性质是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，AB是⊙O的直径，CD是弦，且CD⊥AB，垂足是P．如果CD=4，PB=1，那么直径AB=5．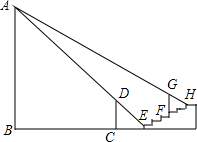
如图，水平地面上竖立着一盏明亮的路灯A，AB垂直地面BC于B．旁边有6级台阶．每级台阶高0.2米，宽0.4米，现有身高1.4米的小明垂直站立在离第一级台阶1.2米的C处时．小明的影子刚好落在第一级台阶的边缘E处．身高0.9米的小华垂直站立在第四级台阶的边缘F处．其影子刚好落在第六级台阶的边缘H处．求路灯AB的高．
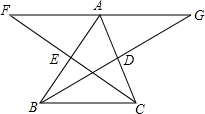已知：如图，BD、CE为△ABC的两条中线，延长BD到G，使BD=DG，延长CE到F，使CE=EF
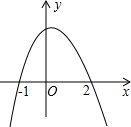如图是抛物线y=-x2+bx+c的图象，根据图象回答下列问题．
16．3.050×106的有效数字（ ），精确到（ ）位．下列选项正确的是（ ）
| A． | 3个，千分位 | B． | 4个，千位 | C． | 2个，万位 | D． | 5个，百位 |