题目内容
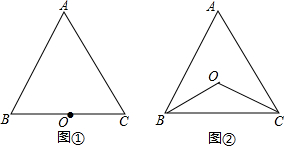
3.已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.(1)如图①,若点O在BC上,求证:∠ABO=∠ACO;
(2)如图②,若点O在△ABC的内部,求证:∠ABO=∠ACO.
分析 (1)先利用斜边直角边定理证明△OEB和△OFC全等,根据全等三角形对应角相等得到∠B=∠C,再根据等边对等角的性质和等式的性质即可得到;
(2)过O作OE⊥AB,OF⊥AC,与(1)的证明思路基本相同.
解答 证明:(1)过点O分别作OE⊥AB,OF⊥AC,E,F分别是垂足,如图①
∵点O到△ABC的两边AB,AC所在直线的距离相等,
∴OE=OF,
又∵OB=OC,
在Rt△OEB与Rt△OFC中
$\left\{\begin{array}{l}{OB=OC}\\{OE=OF}\end{array}\right.$,
∴Rt△OEB≌Rt△OFC(HL),
∴∠B=∠C(全等三角形的对应角相等),
∴∠ABO=∠ACO;
(2)过点O分别作OE⊥AB,OF⊥AC,E,F分别是垂足,如图②
由题意知,OE=OF,
在Rt△OEB和Rt△OFC中,
∵OE=OF,OB=OC,
在Rt△OEB与Rt△OFC中
$\left\{\begin{array}{l}{OB=OC}\\{OE=OF}\end{array}\right.$,
∴Rt△OEB≌Rt△OFC(HL),
∴∠OBE=∠OCF,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠B-∠OBC=∠C-∠OCB,
即∠ABO=∠ACO.
点评 本题考查了全等三角形的判定,全等三角形对应角相等的判定与性质,等角对等边的性质,熟练掌握性质作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.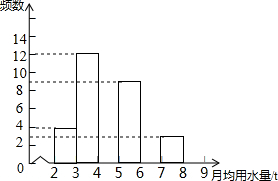 旬阳县在实施定额用水管理前,对城镇6000户居民生活用月均用水情况(单位:t)进行了简单随机抽样调查,并将调查结果绘制成频数分布表和频数分布直方图.
旬阳县在实施定额用水管理前,对城镇6000户居民生活用月均用水情况(单位:t)进行了简单随机抽样调查,并将调查结果绘制成频数分布表和频数分布直方图.
(1)补全频数分布表和频数分布直方图;
(2)用扇形统计图表示各用水段居民户占总居民户的百分比;
(3)为了鼓励居民节约用水,县自来水公司要确定一个用水量的标准,超出这个标准的部分按照2倍的价格收费,且要保证60%以上的家庭水费支出不受影响,你觉得家庭月均用水量应定为多少?为什么?在额定标准下,估计有多少户居民家庭水费支出较前有所增加?
 旬阳县在实施定额用水管理前,对城镇6000户居民生活用月均用水情况(单位:t)进行了简单随机抽样调查,并将调查结果绘制成频数分布表和频数分布直方图.
旬阳县在实施定额用水管理前,对城镇6000户居民生活用月均用水情况(单位:t)进行了简单随机抽样调查,并将调查结果绘制成频数分布表和频数分布直方图.(1)补全频数分布表和频数分布直方图;
(2)用扇形统计图表示各用水段居民户占总居民户的百分比;
(3)为了鼓励居民节约用水,县自来水公司要确定一个用水量的标准,超出这个标准的部分按照2倍的价格收费,且要保证60%以上的家庭水费支出不受影响,你觉得家庭月均用水量应定为多少?为什么?在额定标准下,估计有多少户居民家庭水费支出较前有所增加?
| 月均用水量 | 频数 | 百分比 |
| 2≤x<3 | 4 | 8% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 14 | 28% |
| 5≤x<6 | 9 | 18% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
| 合计 | 50 | 100% |
 如图,线段AB的两个端点坐标分别为A(1,1),B(2,1),以原点O为位似中心,将线段AB放大后得到线段CD,若CD=2,则端点C的坐标为(2,2).
如图,线段AB的两个端点坐标分别为A(1,1),B(2,1),以原点O为位似中心,将线段AB放大后得到线段CD,若CD=2,则端点C的坐标为(2,2). 如图,已知DA∥FE∥CB,且DA=CB,求证:$\frac{EA}{AM}$=$\frac{EB}{BN}$.
如图,已知DA∥FE∥CB,且DA=CB,求证:$\frac{EA}{AM}$=$\frac{EB}{BN}$. 如图,已知AB⊥AC于点A,DC⊥AC于点C,BE平分∠ABD,DE平分∠BDC,BE的延长线交DC的延长线于点F.求证:AB=CF.
如图,已知AB⊥AC于点A,DC⊥AC于点C,BE平分∠ABD,DE平分∠BDC,BE的延长线交DC的延长线于点F.求证:AB=CF. 如图,在△ABC中,AC=4,AB=5,BC=6,点D、E分别在AB、AC上,且∠AED=∠B,如果四边形BCED的周长为13,求DE的长.
如图,在△ABC中,AC=4,AB=5,BC=6,点D、E分别在AB、AC上,且∠AED=∠B,如果四边形BCED的周长为13,求DE的长. 如图,点0是△ABC的∠ABC、∠ACB的平分线的交点,
如图,点0是△ABC的∠ABC、∠ACB的平分线的交点,