题目内容
18. 如图,已知AB⊥AC于点A,DC⊥AC于点C,BE平分∠ABD,DE平分∠BDC,BE的延长线交DC的延长线于点F.求证:AB=CF.
如图,已知AB⊥AC于点A,DC⊥AC于点C,BE平分∠ABD,DE平分∠BDC,BE的延长线交DC的延长线于点F.求证:AB=CF.
分析 先证出AB∥DC,得出∠ABE=∠F,再证出∠F=∠DBF,得出DB=DF,由等腰三角形的三线合一性质得出BE=FE,由ASA证明△ABE≌△FCE,得出对应边相等即可.
解答 证明:∵AB⊥AC于点A,DC⊥AC于点C,
∴AB∥DC,
∴∠ABE=∠F,
∵BE平分∠ABD,
∴∠DBF=∠ABE,
∴∠F=∠DBF,
∴DB=DF,
∵DE平分∠BDC,
∴BE=FE(三线合一),
在△ABE和△FCE中,
$\left\{\begin{array}{l}{∠ABE=∠F}&{\;}\\{BE=FE}&{\;}\\{∠AEB=∠CEF}&{\;}\end{array}\right.$,
∴△ABE≌△FCE(ASA),
∴AB=CF.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质;熟练掌握全等三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
2.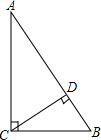 如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,那么以下线段大小的比较中必定成立的是( )
如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,那么以下线段大小的比较中必定成立的是( )
 如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,那么以下线段大小的比较中必定成立的是( )
如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,那么以下线段大小的比较中必定成立的是( )| A. | AD>CD | B. | BC<AC | C. | BC>BD | D. | BD<CD |
 读句画图:如图,A,B,C,D在同一平面内,
读句画图:如图,A,B,C,D在同一平面内, 如图,在△ABC中,$\frac{AB}{DB}$=$\frac{AC}{EC}$.求证:
如图,在△ABC中,$\frac{AB}{DB}$=$\frac{AC}{EC}$.求证: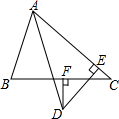 如图,△ABC中,F为BC的中点,FD⊥BC,交∠BAC的平分线于D,DE⊥AC于E,求证:AB+AC=2AE.
如图,△ABC中,F为BC的中点,FD⊥BC,交∠BAC的平分线于D,DE⊥AC于E,求证:AB+AC=2AE.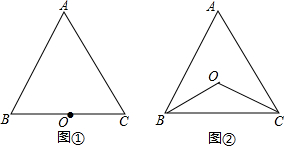
 如图,点P是△ABC三条角平分线的交点,求∠PAC+∠PCB+∠PBA的值.
如图,点P是△ABC三条角平分线的交点,求∠PAC+∠PCB+∠PBA的值.