Question

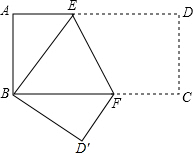
14．如图，Rt△ABC中，AB=AC=4，D为BC中点，E是线段AD上任意一点，将线段EC绕着点E顺时针方向旋转90°，得到线段EF，连接DF，则DF的最小值是2．

Answer 1

分析 连接FC，证明△ACE∽△BCF，由相似三角形的性质得到∠CBF为定值45°，然后分析点F的运动轨迹，再根据题意求DF的最小值

解答 解：如下图所示：连接CF，

∵Rt△ABC中，AB=AC=4，
∴∠ABC=∠ACB=45°，
又∵线段EC绕着点E顺时针方向旋转90°后得到线段EF，
∴∠ECF=∠EFC=45°．
∵∠AEC+∠ECB=∠FCB+∠ECB=45°，
∴∠ACE=∠FCB
又∵$\frac{AC}{BC}=\frac{4}{4\sqrt{2}}=\frac{\sqrt{2}}{2}$，$\frac{EC}{FC}=\frac{EC}{\sqrt{2}EC}=\frac{\sqrt{2}}{2}$，即：$\frac{AC}{BC}=\frac{EC}{FC}$，
∴△ACE∽△BCF
∴∠CBF=∠CAE=45°
则根据垂线段最短知，当DF⊥BF于F时．，DF的值最小．
∵△BDF′是等腰直角三角形，且DB=DF′，∠BDF′=90°，
∴AD=CD=BD=DF′=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{2}$，
又∵在△BDF′中，BD=DF′，∠BDF′=90°，
∴DF=$\frac{\sqrt{2}}{2}$BD=2
  即：DF的最小值为2

点评 本题考查了等腰直角三角形的与旋转的性质，解题的关键是分析清楚点F的运动轨迹．