题目内容
3.若实数m、n满足$\sqrt{m+3}$+|n-2|=0,则过点(m,n)的反比例函数解析式为y=-$\frac{6}{x}$.分析 首先利用非负数的性质求得a、b的值.然后把点(m,n)代入反比例函数解析式来求k的值.
解答 解:设过点(m,n)的反比例函数解析式为y=$\frac{k}{x}$(k≠0).
∵实数m、n满足$\sqrt{m+3}$+|n-2|=0,
∴m=-3,n=2,
∴点(-3,2)在满足反比例函数解析式y=$\frac{k}{x}$(k≠0).
∴k=-3×2=-6,
∴该反比例函数解析式为y=-$\frac{6}{x}$.
故答案是:y=-$\frac{6}{x}$.
点评 此题比较简单,考查的是用待定系数法求反比例函数的解析式,是中学阶段的重点.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
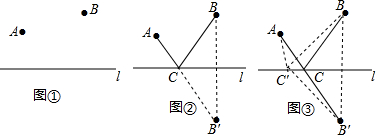
18.下列关于尺规的功能说法不正确的是( )
| A. | 直尺的功能是:在两点间连接一条线段,将线段向两方向延长 | |
| B. | 直尺的功能是:可作平角和直角 | |
| C. | 圆规的功能是:以任意长为半径,以任意点为圆心作一个圆 | |
| D. | 圆规的功能是:以任意长为半径,以任意点为圆心作一段弧 |
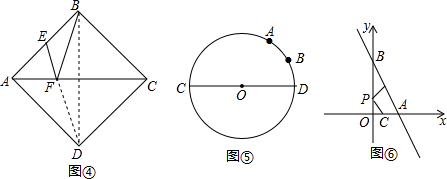
 如图,Rt△ABC中,AB=AC=4,D为BC中点,E是线段AD上任意一点,将线段EC绕着点E顺时针方向旋转90°,得到线段EF,连接DF,则DF的最小值是2.
如图,Rt△ABC中,AB=AC=4,D为BC中点,E是线段AD上任意一点,将线段EC绕着点E顺时针方向旋转90°,得到线段EF,连接DF,则DF的最小值是2. 如图,在平面直角坐标系中,点 P 从原点 O 出发,沿 x 轴向右以每秒1 个单位长的速度运动 t(t>0)秒,抛物线 y=x2+bx+c 经过点 O 和点 P.已知矩形 ABCD 的三个顶点为 A(1,0),B(1,-5),D(4,0).
如图,在平面直角坐标系中,点 P 从原点 O 出发,沿 x 轴向右以每秒1 个单位长的速度运动 t(t>0)秒,抛物线 y=x2+bx+c 经过点 O 和点 P.已知矩形 ABCD 的三个顶点为 A(1,0),B(1,-5),D(4,0). 如图,已知一次函数y=x+2与反比例函数的图象交于两点A和B(a,4)
如图,已知一次函数y=x+2与反比例函数的图象交于两点A和B(a,4)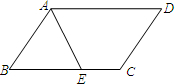 如图,在平行四边形ABCD中,∠A的平分线交BC于点E,若AB=9cm,AD=14cm,则EC=5cm.
如图,在平行四边形ABCD中,∠A的平分线交BC于点E,若AB=9cm,AD=14cm,则EC=5cm.