题目内容
7.不论k为何值,抛物线y=(k-2)x2-2kx+k+3均经过定点M,抛物线与x轴交于两个不同的点A,点B,若∠MAB=45°,则k=-3或5.分析 由y=(k-2)x2-2kx+k+3=K(x2-2x+1)-2x2+3,因为不论k为何值,抛物线y=(k-2)x2-2kx+k+3均经过定点M,所以x2-2x+1=0,解得x=1,可得定点M(1,1),再根据抛物线与x轴交于两个不同的点A,点B,若∠MAB=45°,推出A(0,0)或(1,0)
解答 解:∵y=(k-2)x2-2kx+k+3=K(x2-2x+1)-2x2+3,
∵不论k为何值,抛物线y=(k-2)x2-2kx+k+3均经过定点M,
∴x2-2x+1=0,
解得x=1,
∴定点M(1,1),
∵抛物线与x轴交于两个不同的点A,点B,若∠MAB=45°,
∴A(0,0)或(1,0),
把A(0,0)代入y=(k-2)x2-2kx+k+3,得到k=-3,
把A(2,0)代入y=(k-2)x2-2kx+k+3,k=5
∴满足条件的k的值为-3或5,
故答案为-3或5.
点评 本题考查抛物线与x轴的交点问题、定点问题、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考填空题中的压轴题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
10.如图,两个转盘分别自由转动一次,当停止转动时,两个转盘的指针都指向2的概率为( )


| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
12.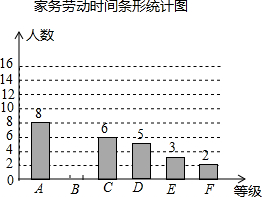 某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:
某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:
家务劳动时间统计表
请根据图表中提供的信息,解答下面的问题:
(1)这次一共调査了40位家长,家务劳动时间统计表中的a=16 ,b=5%;
(2)请把家务劳动时间条形统计图补充完整;
(3)若绘制“家务劳动时间扇形统计图”,等级为“D”所对应扇形的圆心角是45度;
(4)若该中学有3000名学生,估计周末家务劳动时间在40分钟以上的学生有1800人.
 某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:
某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:家务劳动时间统计表
| 等级 | 家务劳动时间 (分钟) | 人数 | 百分比 |
| A | 50以上 | 8 | 20% |
| B | 41-50 | a | 40% |
| C | 31-40 | 6 | 15% |
| D | 21-30 | 5 | 12.5% |
| E | 11-20 | 3 | 7.5% |
| F | 0-10 | 2 | b |
(1)这次一共调査了40位家长,家务劳动时间统计表中的a=16 ,b=5%;
(2)请把家务劳动时间条形统计图补充完整;
(3)若绘制“家务劳动时间扇形统计图”,等级为“D”所对应扇形的圆心角是45度;
(4)若该中学有3000名学生,估计周末家务劳动时间在40分钟以上的学生有1800人.
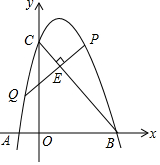 抛物线y=ax2+bx+4交x轴于点A(-1,0),B(3,0),交y轴于点C,点E为BC上的点,过点E的垂线交抛物线于点P,Q,点P在第一象限,若点E为PQ的中点,求点P的坐标.
抛物线y=ax2+bx+4交x轴于点A(-1,0),B(3,0),交y轴于点C,点E为BC上的点,过点E的垂线交抛物线于点P,Q,点P在第一象限,若点E为PQ的中点,求点P的坐标.