题目内容
19.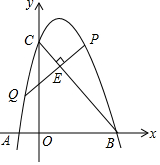 抛物线y=ax2+bx+4交x轴于点A(-1,0),B(3,0),交y轴于点C,点E为BC上的点,过点E的垂线交抛物线于点P,Q,点P在第一象限,若点E为PQ的中点,求点P的坐标.
抛物线y=ax2+bx+4交x轴于点A(-1,0),B(3,0),交y轴于点C,点E为BC上的点,过点E的垂线交抛物线于点P,Q,点P在第一象限,若点E为PQ的中点,求点P的坐标.
分析 首先求出直线PQ的解析式,再利用方程组求出点P的坐标.
解答 解:把A(-1,0),B(3,0)代入y=ax2+bx+4得到$\left\{\begin{array}{l}{a-b+4=0}\\{9a+3b+4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{4}{3}}\\{b=\frac{8}{3}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{4}{3}$x2+$\frac{8}{3}$x+4,
∵C(0,4),B(3,0),
∴直线BC的解析式为y=-$\frac{4}{3}$x+4,
∵PQ⊥BC,
∴可以假设直线PQ的解析式为y=$\frac{3}{4}$x+b′,
由$\left\{\begin{array}{l}{y=\frac{3}{4}x+b′}\\{y=-\frac{4}{3}{x}^{2}+\frac{8}{3}x+4}\end{array}\right.$,消去y得到16x2-23x+12b′-48=0 ①
∵E是PQ的中点,
∴点E的横坐标为$\frac{23}{32}$,纵坐标为$\frac{73}{24}$,
∴E($\frac{23}{32}$,$\frac{73}{24}$),把E代入y=$\frac{3}{4}$x+b′可得b′=$\frac{5}{4}$,
把b′=$\frac{5}{4}$代入①解方程可得x=$\frac{23±\sqrt{2641}}{32}$,
∴P($\frac{23+\sqrt{2641}}{32}$,$\frac{229+3\sqrt{2641}}{248}$).
点评 本题考查二次函数与x轴的交点坐标、一次函数的应用,解题的关键是熟练掌握待定系数法,学会构建方程组求两个函数的交点坐标.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. |  | B. |  | C. |  | D. |  |
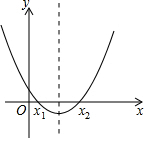 函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )| A. | y=m | B. | y<0 | C. | y>m | D. | 0<y<m |
| A. | S=120-30t (0≤t≤4) | B. | S=120-30t (t>0) | ||
| C. | S=30t (0≤t≤40) | D. | S=30t (t<4) |
| A. | y3<y1<y2 | B. | y3<y2<y1 | C. | y1<y2<y3 | D. | y2<y1<y3 |
 直线y=(2-a)x+3-a在直角坐标系中的图象如图所示,化简|3-a|+|2-a|=2a-5.
直线y=(2-a)x+3-a在直角坐标系中的图象如图所示,化简|3-a|+|2-a|=2a-5.