题目内容
15.在平面直角坐标系xOy中,直线y=kx+b经过点A(3,1),与x轴交于点B,与y轴交于点C,连接OA,若S△AOB:S△BOC═1:2,求直线y=kx+b的解析式.分析 分两种情况考虑:①直线y=k1x+b经过第一、三、四象限,由S△AOB:S△BOC=1:2结合三角形的面积公式得出点C的坐标,由待定系数法即可求出此时直线的函数解析式;②直线y=k1x+b经过第一、二、四象限,由S△AOB:S△BOC=1:2结合三角形的面积公式得出点C的坐标,由待定系数法即可求出此时直线的函数解析式.
解答 解:根据题意,有两种情况:
①直线y=kx+b经过第一、三、四象限,如图1所示.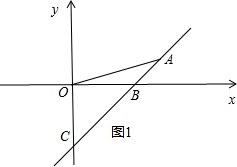
∵S△AOB:S△BOC=1:2,点A(3,1),
∴点C的坐标为(0,-2).
则有$\left\{\begin{array}{l}{b=-2}\\{3k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$.
∴直线的解析式为y=x-2.
②直线y=k1x+b经过第一、二、四象限,如图2所示.
∵S△AOB:S△BOC=1:2,点A(3,1),
∴点C的坐标为(0,2).
则有$\left\{\begin{array}{l}{b=2}\\{3k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=2}\end{array}\right.$.
∴直线的解析式为y=-$\frac{1}{3}$x+2.
点评 本题考查了待定系数法求函数解析式以及三角形的面积公式,解题的关键是分两种情况分别求出点C的坐标.结合点的坐标利用待定系数法求出函数解析式是关键.

练习册系列答案
相关题目
19.我市某连续7天的最高气温为:28°,27°,30°,33°,30°,30°,32°,这组数据的平均数和众数分别是( )
| A. | 28°,30° | B. | 30°,28° | C. | 31°,30° | D. | 30°,30° |
10.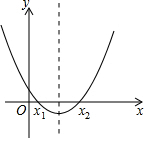 函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
 函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )| A. | y=m | B. | y<0 | C. | y>m | D. | 0<y<m |

 .
.