题目内容
17.某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
分析 (1)设2014年这种礼盒的进价为x元/盒,则2016年这种礼盒的进价为(x-11)元/盒,根据2014年花3500元与2016年花2400元购进的礼盒数量相同,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设年增长率为a,根据数量=总价÷单价求出2014年的购进数量,再根据2014年的销售利润×(1+增长率)2=2016年的销售利润,即可得出关于m的一元二次方程,解之即可得出结论.
解答 解:(1)设2014年这种礼盒的进价为x元/盒,则2016年这种礼盒的进价为(x-11)元/盒,
根据题意得:$\frac{3500}{x}$=$\frac{2400}{x-11}$,
解得:x=35,
经检验,x=35是原方程的解.
答:2014年这种礼盒的进价是35元/盒.
(2)设年增长率为a,
2014年的销售数量为3500÷35=100(盒).
根据题意得:(60-35)×100(1+a)2=(60-35+11)×100,
解得:a=0.2=20%或a=-2.2(不合题意,舍去).
答:年增长率为20%.
点评 本题考查了一元二次方程的应用以及分式方程的应用,解题的关键是:(1)找准等量关系,列出分式方程;(2)找准等量关系,列出一元二次方程.

练习册系列答案
相关题目
8.汽车由A地驶往相距120km的B地,它的平均速度是30km/h,则汽车距B地路程s (km)与行驶时间t(h)的函数关系式及自变量t的取值范围是( )
| A. | S=120-30t (0≤t≤4) | B. | S=120-30t (t>0) | ||
| C. | S=30t (0≤t≤40) | D. | S=30t (t<4) |
9.已知A(-1,y1)、B(-2,y2)、C(1,y3)是一次函数y=b-3x的图象上三点,则大小关系为( )
| A. | y3<y1<y2 | B. | y3<y2<y1 | C. | y1<y2<y3 | D. | y2<y1<y3 |
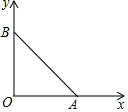 如图,△AOB的顶点A、B分别在x轴,y轴上,∠BAO=45°,且△AOB的面积为8.
如图,△AOB的顶点A、B分别在x轴,y轴上,∠BAO=45°,且△AOB的面积为8.