题目内容
2.若一次函数y=-2x+b的图象与两坐标轴所围成的三角形的面积为9,则函数表达式为y=-2x+6或y=-2x-6.分析 根据题意确定与x轴与y轴的交点,利用三角形的面积公式求出b的值,即可得出答案.
解答 解:直线y=-2x+b与x轴的交点坐标是($\frac{b}{2}$,0),与y轴的交点坐标是(0,b),
根据三角形的面积是9,得到 $\frac{1}{2}$|$\frac{b}{2}$|•|b|=9,即 $\frac{{b}^{2}}{4}$=9,
解得:b=±6,
∴直线解析式为y=-2x+6或y=-2x-6.
故答案为:y=-2x+6或y=-2x-6.
点评 本题主要考查了待定系数法球函数解析式,解题的关键是根据三角形的面积得出b的值.

练习册系列答案
相关题目
5.如图是一个几何体的三视图,则这个几何体是( )


| A. | 三棱柱 | B. | 圆柱 | C. | 圆台 | D. | 圆锥 |
10.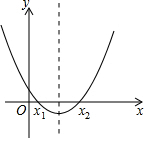 函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
 函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )| A. | y=m | B. | y<0 | C. | y>m | D. | 0<y<m |
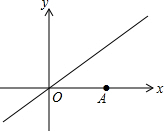 如图,点A坐标为(2,0),在直线y=$\frac{\sqrt{3}}{3}$x上取点M,使△AOM为等腰三角形,则满足条件的M坐标为(-$\sqrt{3}$,-1),($\sqrt{3}$,1),(3,$\sqrt{3}$),(1,$\frac{\sqrt{3}}{3}$).
如图,点A坐标为(2,0),在直线y=$\frac{\sqrt{3}}{3}$x上取点M,使△AOM为等腰三角形,则满足条件的M坐标为(-$\sqrt{3}$,-1),($\sqrt{3}$,1),(3,$\sqrt{3}$),(1,$\frac{\sqrt{3}}{3}$).
 直线y=(2-a)x+3-a在直角坐标系中的图象如图所示,化简|3-a|+|2-a|=2a-5.
直线y=(2-a)x+3-a在直角坐标系中的图象如图所示,化简|3-a|+|2-a|=2a-5.