题目内容
15.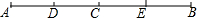 如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.
如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.(1)若线段DE=9cm,求线段AB的长;
(2)在(1)中,延长AB到O,使BO=$\frac{3}{4}$AB,求线段AO的长.
分析 (1)根据中点的性质得到DE=$\frac{1}{2}$AB,计算即可;
(2)根据题意求出BO的长,根据AO=AB+BO计算即可.
解答 解:(1)∵点C是线段AB的中点,
∴AC=BC=$\frac{1}{2}$AB,
∵点D是线段AC的中点,
∴DC=$\frac{1}{2}$AC=$\frac{1}{4}$AB,
∵点E是线段BC的中点,
∴CE=$\frac{1}{2}$CB=$\frac{1}{4}$AB,
∴DE=DC+CE=$\frac{1}{2}$AB=9cm,
∴AB=18cm;
(2)∵BO=$\frac{3}{4}$AB,AB=18cm,
∴BO=13.5cm,
∴AO=AB+BO=31.5cm.
点评 本题考查的是两点间的距离线段中点的性质,灵活运用中点的性质是解题的关键,注意数形结合思想的正确运用.

练习册系列答案
相关题目
20. 如图,平行四边形ABCD的对角线BD的长为4cm,将平行四边形ABCD绕其对角线的交点O旋转180°,则点B所经过的路径长为( )
如图,平行四边形ABCD的对角线BD的长为4cm,将平行四边形ABCD绕其对角线的交点O旋转180°,则点B所经过的路径长为( )
 如图,平行四边形ABCD的对角线BD的长为4cm,将平行四边形ABCD绕其对角线的交点O旋转180°,则点B所经过的路径长为( )
如图,平行四边形ABCD的对角线BD的长为4cm,将平行四边形ABCD绕其对角线的交点O旋转180°,则点B所经过的路径长为( )| A. | 4πcm | B. | 3πcm | C. | 2πcm | D. | πcm |
7.关于x的方程x2+2kx-1=0的根的情况描述正确的是( )
| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
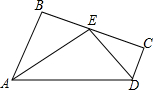 如图,AB∥CD,E点在BC上,AE平分∠BAD,DE平分∠ADC.求证:
如图,AB∥CD,E点在BC上,AE平分∠BAD,DE平分∠ADC.求证: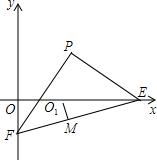 如图,P(1,1),PE⊥PF,O为△OEF的内角平分线的交点,O1M⊥EF于M.
如图,P(1,1),PE⊥PF,O为△OEF的内角平分线的交点,O1M⊥EF于M. 如图,点A、B、C顺次在直线l上,点M是线段AC的中点,点N是线段BC的中点,NC=2cm,AB=8cm,求AM的长.
如图,点A、B、C顺次在直线l上,点M是线段AC的中点,点N是线段BC的中点,NC=2cm,AB=8cm,求AM的长.