题目内容
15. 如图,将?ABCD的边DC延长到点E,使CE=DC,连结AE,交BC于点F.
如图,将?ABCD的边DC延长到点E,使CE=DC,连结AE,交BC于点F.(1)求证:BF=$\frac{1}{2}$BC;
(2)若∠AFC=2∠D,连结AC,BE,求证:四边形ABEC是矩形.
分析 (1)根据平行四边形的性质得到AB∥CD,AB=CD,然后根据CE=DC,得到AB=EC,AB∥EC,即可证得四边形ABEC是平行四边形,继而证得结论;
(2)由(1)得的结论先证得四边形ABEC是平行四边形,通过角的关系得出FA=FE=FB=FC,AE=BC,得证.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵CE=DC,
∴AB=EC,
∴四边形ABEC是平行四边形,
∴BF=$\frac{1}{2}$BC;
(2)∵由(1)知,四边形ABEC是平行四边形,
∴FA=FE,FB=FC.
∵四边形ABCD是平行四边形,
∴∠ABC=∠D.
又∵∠AFC=2∠ADC,
∴∠AFC=2∠ABC.
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
点评 此题考查了平行四边形的判定与性质以及矩形的判定.关键是利用平行四边形的性质,通过角的关系证矩形.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
10. 如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
 如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
如图,DE是△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )| A. | 2.5 | B. | 1.5 | C. | 4 | D. | 5 |
4.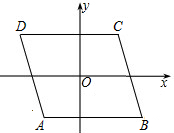 如图,以?ABCD对角线的交点O为坐标原点,以平行于AB边的直线为x轴,建立平面直角坐标系.若点B的坐标为(3,-2),则点D的坐标为( )
如图,以?ABCD对角线的交点O为坐标原点,以平行于AB边的直线为x轴,建立平面直角坐标系.若点B的坐标为(3,-2),则点D的坐标为( )
 如图,以?ABCD对角线的交点O为坐标原点,以平行于AB边的直线为x轴,建立平面直角坐标系.若点B的坐标为(3,-2),则点D的坐标为( )
如图,以?ABCD对角线的交点O为坐标原点,以平行于AB边的直线为x轴,建立平面直角坐标系.若点B的坐标为(3,-2),则点D的坐标为( )| A. | (2,-3) | B. | (-2,3) | C. | (-3,-2) | D. | (-3,2) |
5. 如图,直线AB、CD相交于点O,OE平分∠AOD,若∠DOE=36°,则∠BOC的度数为( )
如图,直线AB、CD相交于点O,OE平分∠AOD,若∠DOE=36°,则∠BOC的度数为( )
 如图,直线AB、CD相交于点O,OE平分∠AOD,若∠DOE=36°,则∠BOC的度数为( )
如图,直线AB、CD相交于点O,OE平分∠AOD,若∠DOE=36°,则∠BOC的度数为( )| A. | 72° | B. | 90° | C. | 108° | D. | 144° |
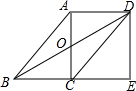 如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,延长BC到点E,使得BC=CE,连结DE.
如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,延长BC到点E,使得BC=CE,连结DE.