Question

20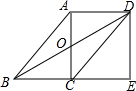．如图，在?ABCD中，对角线AC，BD交于点O，AC⊥BC，延长BC到点E，使得BC=CE，连结DE．
（1）求证：四边形ACED是矩形；
（2）若AC=4，BD=6，求CD的长．

Answer 1

分析 （1）由四边形ABCD是平行四边形，BC=CE，易证得四边形ACED是平行四边形，又由AC⊥BC，即可证得四边形ACED是矩形；
（2）由四边形ACED是矩形，AC=4，BD=6，利用勾股定理即可求得BE的长，继而求得答案．

解答 （1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵BC=CE，
∴AD=CE，
∴四边形ACED是平行四边形，
∵AC⊥BC，
∴∠ACE=90°，
∴四边形ACED是矩形；

（2）∵四边形ACED是矩形，
∴DE=AC=4，∠E=90°，
∴BE=$\sqrt{B{D}^{2}-D{E}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$，
∵BC=CE，
∴CE=$\frac{1}{2}$BE=$\sqrt{5}$，
∴CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=$\sqrt{21}$．

点评 此题考查了矩形的判定与性质以及勾股定理．注意利用勾股定理求线段CD的长是关键．