题目内容
2. 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
分析 (1)在直角三角形DCE中,利用锐角三角函数定义求出DE的长即可;
(2)过D作DF垂直于AB,交AB于点F,可得出三角形BDF为等腰直角三角形,设BF=DF=x,表示出BC,BD,DC,由题意得到三角形BCD为直角三角形,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出AB的长.
解答  解:(1)在Rt△DCE中,DC=4米,∠DCE=30°,∠DEC=90°,
解:(1)在Rt△DCE中,DC=4米,∠DCE=30°,∠DEC=90°,
∴DE=$\frac{1}{2}$DC=2米;
(2)过D作DF⊥AB,交AB于点F,
∵∠BFD=90°,∠BDF=45°,
∴∠BFD=45°,即△BFD为等腰直角三角形,
设BF=DF=x米,
∵四边形DEAF为矩形,
∴AF=DE=2米,即AB=(x+2)米,
在Rt△ABC中,∠ABC=30°,
∴BC=$\frac{AB}{cos30°}$=$\frac{x+2}{\frac{\sqrt{3}}{2}}$=$\frac{2x+4}{\sqrt{3}}$=$\frac{\sqrt{3}(2x+4)}{3}$米,
BD=$\sqrt{2}$BF=$\sqrt{2}$x米,DC=4米,
∵∠DCE=30°,∠ACB=60°,
∴∠DCB=90°,
在Rt△BCD中,根据勾股定理得:2x2=$\frac{(2x+4)^{2}}{3}$+16,
解得:x=4+4$\sqrt{3}$,
则AB=(6+4$\sqrt{3}$)米.
点评 此题考查了解直角三角形-仰角俯角问题,坡度坡角问题,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
17.三张外观相同的卡片分别标有数字1、2、3,从中随机一次抽出两张,这两张卡片上的数字恰好都小于3的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
7.据统计,从2005年到2015年中国累积节能1570000000吨标准煤,1570000000这个数用科学记数法表示为( )
| A. | 0.157×1010 | B. | 1.57×108 | C. | 1.57×109 | D. | 15.7×108 |
11.地球上的海洋面积为361 000 000平方千米,数字361 000 000用科学记数法表示为( )
| A. | 36.1×107 | B. | 0.361×109 | C. | 3.61×108 | D. | 3.61×107 |
 如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.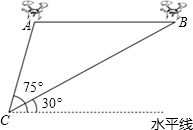 某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)