题目内容
12.在△ABC中,∠C=90°,∠A=30°,AB=16,则AC等于8$\sqrt{3}$.分析 根据直角三角形30°角所对的直角边等于斜边的一半求出BC,然后利用勾股定理列式计算即可得解.
解答  解:∵在△ABC中,∠C=90°,∠A=30°,AB=16,
解:∵在△ABC中,∠C=90°,∠A=30°,AB=16,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×16=8,
由勾股定理得,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{6}^{2}-{8}^{2}}$=8$\sqrt{3}$.
故答案为:8$\sqrt{3}$.
点评 本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理的应用,熟记性质是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
20.我市气象部门测得某周内七天的日温差数据如下:4,6,6,5,7,6,8(单位:℃),这组数据的平均数和众数分别是( )
| A. | 7,6 | B. | 6,5 | C. | 5,6 | D. | 6,6 |
7.下列图形都是由同样大小的基本图形按一定规律所组成的,其中第①个图形中一共有5个基本图形,第②个图形中一共有8个基本图形,第③个图形中一共有11个基本图形,第④个图形中一共有14个基本图形,…,按此规律排列,则第⑧个图形中基本图形的个数为( )
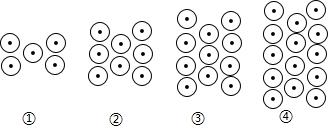

| A. | 23 | B. | 24 | C. | 26 | D. | 29 |
17.下列备选答案的四个数中,最大的一个是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
4.下列计算中,正确的是( )
| A. | (-ab)2=a2b2 | B. | a•a3=a3 | C. | a6÷a2=a3 | D. | 2a+3b=5ab |
1.已知α为锐角,sinα=$\frac{1}{2}$,则α等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
2.下列运算中,结果正确的是( )
| A. | 2a+3b=5ab | B. | a2•a3=a6 | C. | (a4)2=a8 | D. | a6÷a3=a2 |
 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.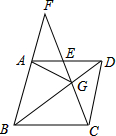 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.