题目内容
10.先化简,再求代数式($\frac{2}{a+1}$-$\frac{2a-3}{{a}^{2}-1}$)÷$\frac{1}{a+1}$的值,其中a=2sin60°+tan45°.分析 先算括号里面的,再算除法,最后把a的值代入进行计算即可.
解答 解:原式=[$\frac{2}{a+1}$-$\frac{2a-3}{(a+1)(a-1)}$]•(a+1)
=$\frac{2(a-1)-2a+3}{(a+1)(a-1)}$•(a+1)
=$\frac{2a-2-2a+3}{(a+1)(a-1)}$•(a+1)
=$\frac{1}{(a+1)(a-1)}$•(a+1)
=$\frac{1}{a-1}$,
当a=2sin60°+tan45°=2×$\frac{\sqrt{3}}{2}$+1=$\sqrt{3}$+1时,原式=$\frac{1}{\sqrt{3}+1-1}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
1.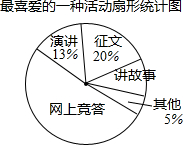 近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
 近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:最喜爱的一种活动统计表
| 活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
| 人数 | 60 | 30 | 39 | a | b |
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
18.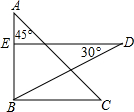 把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
 把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )| A. | 内部 | B. | 外部 | C. | 边上 | D. | 以上都有可能 |
5. 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
请根据以上信息解答下列问题:
(1)填空:m=4,n=1;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在B组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 3 |
| E | 9500≤x<10500 | n |
(1)填空:m=4,n=1;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在B组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
15.面积为2的正方形的边长在( )
| A. | 0和1之间 | B. | 1和2之间 | C. | 2和3之间 | D. | 3和4之间 |
19.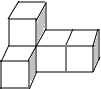 由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
 由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )| A. | 主视图的面积最小 | B. | 左视图的面积最小 | ||
| C. | 俯视图的面积最小 | D. | 三个视图的面积相等 |
20.我市气象部门测得某周内七天的日温差数据如下:4,6,6,5,7,6,8(单位:℃),这组数据的平均数和众数分别是( )
| A. | 7,6 | B. | 6,5 | C. | 5,6 | D. | 6,6 |

 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.