题目内容
14.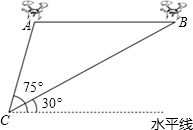 某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
分析 如图,作AD⊥BC,BH⊥水平线,根据题意确定出∠ABC与∠ACB的度数,利用锐角三角函数定义求出AD与BD的长,由CD+BD求出BC的长,即可求出BH的长.
解答 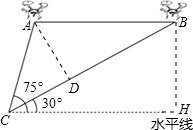 解:如图,作AD⊥BC,BH⊥水平线,
解:如图,作AD⊥BC,BH⊥水平线,
由题意得:∠ACH=75°,∠BCH=30°,AB∥CH,
∴∠ABC=30°,∠ACB=45°,
∵AB=32m,
∴AD=CD=16m,BD=AB•cos30°=16$\sqrt{3}$m,
∴BC=CD+BD=(16$\sqrt{3}$+16)m,
则BH=BC•sin30°=(8$\sqrt{3}$+8)m.
点评 此题考查了解直角三角形的应用-仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
请根据以上信息解答下列问题:
(1)填空:m=4,n=1;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在B组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 3 |
| E | 9500≤x<10500 | n |
(1)填空:m=4,n=1;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在B组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
9.施工队要铺设一段全长2000米的管道,因在中考期间需停工两天,实际每天施工需比原计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x米,则根据题意所列方程正确的是( )
| A. | $\frac{2000}{x}$-$\frac{2000}{x+50}$=2 | B. | $\frac{2000}{x+50}$-$\frac{2000}{x}$=2 | ||
| C. | $\frac{2000}{x}$-$\frac{2000}{x-50}$=2 | D. | $\frac{2000}{x-50}$-$\frac{2000}{x}$=2 |
19.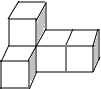 由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
 由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )| A. | 主视图的面积最小 | B. | 左视图的面积最小 | ||
| C. | 俯视图的面积最小 | D. | 三个视图的面积相等 |
4.下列计算中,正确的是( )
| A. | (-ab)2=a2b2 | B. | a•a3=a3 | C. | a6÷a2=a3 | D. | 2a+3b=5ab |

 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.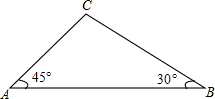 如图,天星山山脚下西端A处与东端B处相距800(1+$\sqrt{3}$)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为$\frac{\sqrt{2}}{2}$米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
如图,天星山山脚下西端A处与东端B处相距800(1+$\sqrt{3}$)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为$\frac{\sqrt{2}}{2}$米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?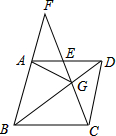 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.