题目内容
12. 如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.
如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.(1)判断四边形CEGF的形状,并证明你的结论;
(2)若AB=3,BC=9,求线段CE的取值范围.
分析 (1)由四边形ABCD是矩形,根据折叠的性质,易证得△EFG是等腰三角形,即可得GF=EC,又由GF∥EC,即可得四边形CEGF为平行四边形,根据邻边相等的平行四边形是菱形,即可得四边形BGEF为菱形;
(2)如图2,当G与A重合时,CE取最大值,由折叠的性质得CD=DG,∠CDE=∠GDE=45°,推出四边形CEGD是矩形,根据矩形的性质即可得到CE=CD=AB=3;如图1,当F与D重合时,CE取最小值,由折叠的性质得AE=CE,根据勾股定理即可得到结论.
解答 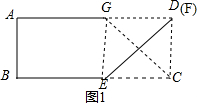 (1)证明:∵四边形ABCD是矩形,
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GFE=∠FEC,
∵图形翻折后点G与点C重合,EF为折线,
∴∠GEF=∠FEC,
∴∠GFE=∠FEG,
∴GF=GE,
∵图形翻折后BC与GE完全重合,
∴BE=EC,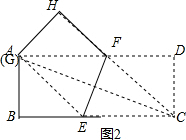
∴GF=EC,
∴四边形CEGF为平行四边形,
∴四边形CEGF为菱形;
(2)由(1)得四边形CEGF是菱形,
∴CE=CD=AB=3;
如图2,当G与A重合时,CE取最大值,
由折叠的性质得AE=CE,
∵∠B=90°,
∴AE2=AB2+BE2,即CE2=32+(9-CE)2,
∴CE=5,
∴线段CE的取值范围3≤CE≤5.
点评 本题考查了翻折变换-折叠问题,菱形的判定,线段的最值问题,矩形的性质,勾股定理,正确的作出图形是解题的关键.

练习册系列答案
相关题目
17. 一个几何体的三视图如图所示,则该几何体的表面积为( )
一个几何体的三视图如图所示,则该几何体的表面积为( )
 一个几何体的三视图如图所示,则该几何体的表面积为( )
一个几何体的三视图如图所示,则该几何体的表面积为( )| A. | 4π | B. | 3π | C. | 2π+4 | D. | 3π+4 |
1.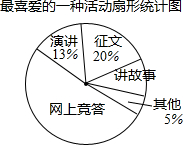 近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
 近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:最喜爱的一种活动统计表
| 活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
| 人数 | 60 | 30 | 39 | a | b |
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.


 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.