题目内容
 如图,?ABCD,连结D和BC的中点E,交AB的延长线于F,求证:AB=BF.
如图,?ABCD,连结D和BC的中点E,交AB的延长线于F,求证:AB=BF.考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:利用平行四边形的性质得出CD∥AB,CD=AB,进而求出△DCE≌△FBE,得出CD=BF,进而求出AB=BF.
解答: 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,
∴∠C=∠CBF,∠CDE=∠F,
∵E是BC的中点,
∴BC=BE,
在△DCE和△FBE中,
,
∴△DCE≌△FBE(AAS),
∴CD=BF,
∵CD=AB,
∴AB=EF.
 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,
∴∠C=∠CBF,∠CDE=∠F,
∵E是BC的中点,
∴BC=BE,
在△DCE和△FBE中,
|
∴△DCE≌△FBE(AAS),
∴CD=BF,
∵CD=AB,
∴AB=EF.
点评:此题主要考查了平行四边形的性质以及全等三角形的判定与性质,得出△DCE≌△FBE是解题关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
下列调查中,适宜采用普查方式的是( )
| A、调查市场上酸奶的质量情况 |
| B、调查我市中小学生的视力情况 |
| C、调查某品牌圆珠笔芯的使用寿命 |
| D、调查乘坐飞机的旅客是否携带危禁物品 |

 已知∠α,利用尺规作∠AOB,使∠AOB=2∠α,请写出作法并作出图形(保留作图痕迹).
已知∠α,利用尺规作∠AOB,使∠AOB=2∠α,请写出作法并作出图形(保留作图痕迹).


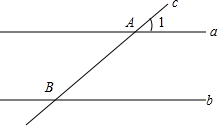 如图,直线a∥b,直线与直线a、b分别交与点A、B且∠1=45°.
如图,直线a∥b,直线与直线a、b分别交与点A、B且∠1=45°.