题目内容
6.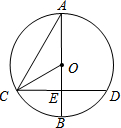 如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 8 |
分析 ⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,由垂径定理可得AB⊥CD,∠A=30°,由圆周角定理得∠COB=60°,则OE=$\frac{1}{2}$OC=2,利用勾股定理可得CD.
解答 解:∵⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,
∴AB⊥CD,
∵∠A=30°,
∴∠COB=60°,
∴OE=$\frac{1}{2}OC$=2,
∴CE=$\sqrt{{4}^{2}{-2}^{2}}$=2$\sqrt{3}$,
∴CD=4$\sqrt{3}$.
故选C.
点评 本题主要考查了圆周角定理,垂径定理和勾股定理,熟练运用垂径定理是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列二次根式中能与$\sqrt{2}$合并的二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
17. 如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
 如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )| A. | 9cm | B. | $6\sqrt{3}$cm | C. | $\frac{9}{2}$cm | D. | $3\sqrt{3}$cm |
1.随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 18000元 |
| 第二周 | 4台 | 10台 | 31000元 |
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
18.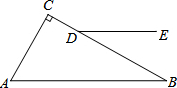 如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
 如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
 如图,在⊙O中,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连接CD.
如图,在⊙O中,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连接CD.