题目内容
16. 如图,在⊙O中,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连接CD.
如图,在⊙O中,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连接CD.(1)求证:CD与⊙O相切;
(2)若CD=6,求弓形BC(劣弧所对)的面积.(结果保留π和根号)
分析 (1)根据已知条件求得△OBC是等边三角形,进而求得∠BCD=∠D=30°,从而求得∠OCD=∠OCB+∠BCD=60°+30°=90°,即可证得结论;
(2)根据正切函数求得半径,然后根据弓形BC(劣弧所对)的面积:S扇形-S△OCB即可求得.
解答 解:(1)∵OA=OB,∠AOB=150°
∴∠A=∠OBA=15°,
∴∠ABC=45°,
∴∠OBC=60°,
∵OC=OB,
∴△OBC是等边三角形,
∴OB=BC,
∵BD=OB,
∴BC=BD,
∴∠BCD=∠D=30°,
∴∠OCD=∠OCB+∠BCD=60°+30°=90°,
∴CD与⊙O相切;
(2)在RT△OCD中,CD=6,
∴OC=CD•tan∠D=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
∴S△OCD=$\frac{1}{2}$OC•CD=$\frac{1}{2}$×$2\sqrt{3}$×6=6$\sqrt{3}$,
∴S△OCB=$\frac{1}{2}$S△OCD=3$\sqrt{3}$,
∴弓形BC(劣弧所对)的面积:S扇形-S△OCB=$\frac{60π×(2\sqrt{3})^{2}}{360}$-3$\sqrt{3}$=2π-3$\sqrt{3}$.
点评 本题考查了切线的判定,正切函数的应用,等边三角形的判定和性质,等腰三角形的判定和性质,扇形的面积等,熟练掌握性质定理是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
6.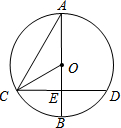 如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
 如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 8 |
 如图,?ABCD中AD=2AB,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为4.
如图,?ABCD中AD=2AB,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为4. 如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为20$\sqrt{2}$海里.
如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为20$\sqrt{2}$海里. 如图,图中的几何体是将圆柱沿竖直方向切掉一半后,再在中心挖去一个圆柱得到的,则该几何体的左视图是( )
如图,图中的几何体是将圆柱沿竖直方向切掉一半后,再在中心挖去一个圆柱得到的,则该几何体的左视图是( )



