题目内容
15.某公司生产的商品的市场指导价为每件150元,公司的实际销售价格可以浮动x个百分点(即销售价格=150(1+x%)),经过市场调研发现,这种商品的日销售量y(件)与销售价格浮动的百分点x之间的函数关系为y=-2x+24.若该公司按浮动-12个百分点的价格出售,每件商品仍可获利10%.(1)求该公司生产销售每件商品的成本为多少元?
(2)当实际销售价格定为多少元时,日销售利润为660元?(说明:日销售利润=(销售价格一成本)×日销售量)
(3)该公司决定每销售一件商品就捐赠a元利润(a≥1)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于-2时,扣除捐赠后的日销售利润随x增大而减小,直接写出a的取值范围.
分析 (1)设该公司生产销售每件商品的成本为z元,根据该公司按浮动-12个百分点的价格出售,每件商品仍可获利10%列出方程,求出方程的解得到z的值,即为每件商品的成本;
(2)根据日销售利润=(销售价格一成本)×日销售量,由日销售利润为660元列出关于x的方程,求出方程的解即可得到结果;
(3)根据题意确定出a的范围即可.
解答 解:(1)设该公司生产销售每件商品的成本为z元,
依题意得:150(1-12%)=(1+10%)z,
解得:z=120,
答:该公司生产销售每件商品的成本为120元;
(2)由题意得(-2x+24)[150(1+x%)-120]=660,
整理得:x2+8x-20=0,
解得:x1=2,x2=-10,
此时,商品定价为每件135元或153元,日销售利润为660元;
(3)根据题意得:1≤a≤6.
点评 此题考查了一元二次方程的应用,以及一次函数的应用,弄清题意是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.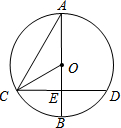 如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
 如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 8 |
10.方程x2-x+1=0与方程x2-5x-1=0的所有实数根的和是( )
| A. | 6 | B. | 5 | C. | 3 | D. | 2 |
20.全球可被人类利用的淡水总量约占地球上总水量的0.00003.其中数字0.00003用科学记数法表示为( )
| A. | 0.3×10-4 | B. | 3×10-4 | C. | 0.3×10-5 | D. | 3×10-5 |
 如图所示,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短.
如图所示,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短.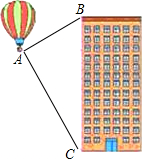 如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为160$\sqrt{3}$米.
如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为160$\sqrt{3}$米. 如图,?ABCD中AD=2AB,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为4.
如图,?ABCD中AD=2AB,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为4. 如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为20$\sqrt{2}$海里.
如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为20$\sqrt{2}$海里.