题目内容
17. 如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )| A. | 9cm | B. | $6\sqrt{3}$cm | C. | $\frac{9}{2}$cm | D. | $3\sqrt{3}$cm |
分析 弦AB垂直平分OC于点D,得OD=3,由勾股定理得AD,由垂径定理得AB=2AD,可得答案.
解答 解:∵⊙O的半径长6cm,弦AB垂直平分OC,
∴OD=3,
由勾股定理得,
AD=$\sqrt{{6}^{2}{-3}^{2}}$=3$\sqrt{3}$,
∴AB=6$\sqrt{3}$,
故选B.
点评 本题主要考查了垂径定理,勾股定理,利用弦AB垂直平分OC得OD是解答此题的关键.

练习册系列答案
相关题目
12.下面的几何体中,俯视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.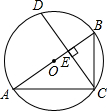 如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )
 如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )| A. | 6 | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
6.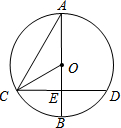 如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
 如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 8 |
 如图所示,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短.
如图所示,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短.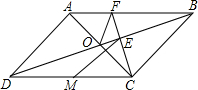 已知?ABCD中,对角线AC、BD相交于点O,且AC⊥AD,∠ADC=45°,过点C作CE⊥BD于点E,交AB于点F,连接OF,点M为CD的中点,连接EM.
已知?ABCD中,对角线AC、BD相交于点O,且AC⊥AD,∠ADC=45°,过点C作CE⊥BD于点E,交AB于点F,连接OF,点M为CD的中点,连接EM. 如图,?ABCD中AD=2AB,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为4.
如图,?ABCD中AD=2AB,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为4.