题目内容
 如图,直线y=kx+b与双曲线y=
如图,直线y=kx+b与双曲线y=| m |
| x |
(1)求出k、b、m的值;
(2)根据图象直接写出不等式kx+b<
| m |
| x |
(3)若点E在x轴的正半轴上,是否存在以点E、C、B构成的三角形与△OAB相似?若存在,请求出E的坐标;若不存在,请说明理由.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)利用待定系数法即可求解;
(2)不等式的解就是对相同的x的值,反比例函数的图象在上边的部分,对应的x的范围;
(3)求得△OAB的边长,点E在x轴的正半轴上,可以分E在线段OC上(不在O点)或线段OC的延长线上两种情况讨论,依据相似三角形的对应边的比相等即可求得.
(2)不等式的解就是对相同的x的值,反比例函数的图象在上边的部分,对应的x的范围;
(3)求得△OAB的边长,点E在x轴的正半轴上,可以分E在线段OC上(不在O点)或线段OC的延长线上两种情况讨论,依据相似三角形的对应边的比相等即可求得.
解答:解:(1)把点A(-1,-5)、D(5,1)代入y=kx+b得
,
解得:
.
把点D(5,1)代入y=
,得m=5;
(2)x<-1或0<x<5;
(3)OA=
=
,
在y=x-4中,令x=0,解得y=-4,则B的坐标是(0,-4).
令y=0,解得:x=4,则C的坐标是(4,0).
故OB=4,AB=
=
,BC=4
,OC=4.
∴OB=OC,即△OBC是等腰直角三角形,
∴∠OCB=∠OBC=45°,∠BCE=135°.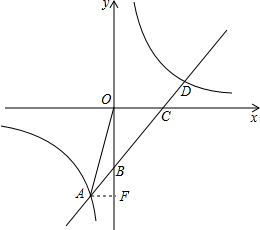
过A作AF⊥y轴于点F.则△ABF是等腰直角△,∠ABF=45°,∠ABO=135°.
1)当E在线段OC(不与O重合)上时,两个三角形一定不能相似;
2)当E在线段OC的延长线上时,设D的坐标是(x,0),则CE=x-4,
∠ABO=∠BCE=135°,
当△AOB∽△EBC时,
=
,即
=
,
解得:x=6,
则E的坐标是(6,0);
当△AOB∽△BEC时,
=
,即
=
,
解得:x=20,
则E的坐标是(20,0).
则E的坐标是(6,0)或(20,0).
|
解得:
|
把点D(5,1)代入y=
| m |
| x |
(2)x<-1或0<x<5;
(3)OA=
| 12+52 |
| 26 |
在y=x-4中,令x=0,解得y=-4,则B的坐标是(0,-4).
令y=0,解得:x=4,则C的坐标是(4,0).
故OB=4,AB=
| 12+(5-4)2 |
| 2 |
| 2 |
∴OB=OC,即△OBC是等腰直角三角形,
∴∠OCB=∠OBC=45°,∠BCE=135°.

过A作AF⊥y轴于点F.则△ABF是等腰直角△,∠ABF=45°,∠ABO=135°.
1)当E在线段OC(不与O重合)上时,两个三角形一定不能相似;
2)当E在线段OC的延长线上时,设D的坐标是(x,0),则CE=x-4,
∠ABO=∠BCE=135°,
当△AOB∽△EBC时,
| OB |
| CB |
| AB |
| EC |
| 4 | ||
4
|
| 2 |
| x-4 |
解得:x=6,
则E的坐标是(6,0);
当△AOB∽△BEC时,
| OB |
| EC |
| AB |
| BC |
| x |
| x-4 |
| ||
4
|
解得:x=20,
则E的坐标是(20,0).
则E的坐标是(6,0)或(20,0).
点评:本题是一次函数、反比例函数与相似三角形的判定与性质的综合应用,注意到∠ABO=∠BCE=135°是本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
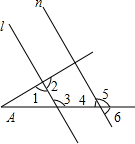 图中直线l、n分别截∠A的两边,且l∥n,∠3=∠1+∠4.根据图中标示的角,判断下列各角的度数关系中正确的是( )
图中直线l、n分别截∠A的两边,且l∥n,∠3=∠1+∠4.根据图中标示的角,判断下列各角的度数关系中正确的是( )| A、∠2+∠5>180° |
| B、∠2+∠3<180° |
| C、∠1+∠6>180° |
| D、∠3+∠4<180° |
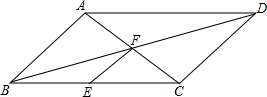 如图,在平行四边形ABCD中,F是对角线的交点,E是边BC的中点,连接EF.
如图,在平行四边形ABCD中,F是对角线的交点,E是边BC的中点,连接EF.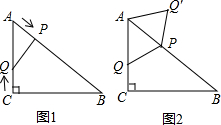 如图1,Rt△ABC中,AC=6cm,BC=8cm,点P以2cm/s的速度从A处沿AB方向匀速运动,点Q以1cm/s的速度从C处沿CA方向匀速运动.连接PQ,若设运动的时间为t(s)(0<t<5).解答下列问题:
如图1,Rt△ABC中,AC=6cm,BC=8cm,点P以2cm/s的速度从A处沿AB方向匀速运动,点Q以1cm/s的速度从C处沿CA方向匀速运动.连接PQ,若设运动的时间为t(s)(0<t<5).解答下列问题: