题目内容
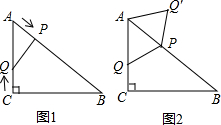 如图1,Rt△ABC中,AC=6cm,BC=8cm,点P以2cm/s的速度从A处沿AB方向匀速运动,点Q以1cm/s的速度从C处沿CA方向匀速运动.连接PQ,若设运动的时间为t(s)(0<t<5).解答下列问题:
如图1,Rt△ABC中,AC=6cm,BC=8cm,点P以2cm/s的速度从A处沿AB方向匀速运动,点Q以1cm/s的速度从C处沿CA方向匀速运动.连接PQ,若设运动的时间为t(s)(0<t<5).解答下列问题:(1)当t为何值时,△APQ与△ABC相似?
(2)设四边形BCQP的面积为y,求出y与t的函数关系式,并求当t为何值时,y的值最小,写出最小值;
(3)如图2,将△APQ沿AP翻折,使点Q落在Q′处,连接AQ′,PQ′,若四边形AQPQ′是平行四边形,求t的值.
考点:相似形综合题
专题:
分析:(1)首先在Rt△ABC中利用勾股定理求得AB=10cm;然后由相似三角形的对应边成比例求得t的值.在△APQ与△ABC中,由一个公共角,所以分两种情况进行讨论:△APQ∽△ABC或△APQ∽△ACB;
(2)如答图2,过点Q作QD⊥AP,垂足为D.构建相似三角形:Rt△ADQ∽Rt△ACB,根据该相似三角形的对应边成比例得到:QD=
=
(6-t).结合图形知道
y=S△ABC-S△APQ,由此列出y关于t的二次函数,利用二次函数的性质进行解答;
(3)若四边形AQPQ′是平行四边形,则四边形AQPQ′一定是菱形.如答图3,连接QQ′交AP于点E.由“菱形的对角线互相垂直且平分”和相似三角形的判定推知
Rt△AEQ∽Rt△ACB,所以根据该相似三角形的对应边成比例来求相应的t的值.
(2)如答图2,过点Q作QD⊥AP,垂足为D.构建相似三角形:Rt△ADQ∽Rt△ACB,根据该相似三角形的对应边成比例得到:QD=
| AQ•BC |
| AB |
| 4 |
| 5 |
y=S△ABC-S△APQ,由此列出y关于t的二次函数,利用二次函数的性质进行解答;
(3)若四边形AQPQ′是平行四边形,则四边形AQPQ′一定是菱形.如答图3,连接QQ′交AP于点E.由“菱形的对角线互相垂直且平分”和相似三角形的判定推知
Rt△AEQ∽Rt△ACB,所以根据该相似三角形的对应边成比例来求相应的t的值.
解答: 解:(1)当t=
解:(1)当t=
或t=
时,△APQ与△ABC相似.理由如下:
∵如答图1,Rt△ABC中,AC=6cm,BC=8cm,
∴由勾股定理知 AB=
=10cm.
由题意知,CQ=t,AQ=6-t,AP=2t.
若△APQ与△ABC相似时,分两种情况:△APQ∽△ABC或△APQ∽△ACB.
①当△APQ∽△ABC时,
=
,即
=
,
解得 t=
;
②当△APQ∽△ACB时,
=
,即
=
,
解得 t=
.
综上所述,当t=
或t=
时,△APQ与△ABC相似;
(2)如答图2,过点Q作QD⊥AP,垂足为D.
∵∠A=∠A,AC⊥BC,
∴Rt△ADQ∽Rt△ACB,
∴
=
,
∴QD=
=
(6-t).
由题意得:y=S△ABC-S△APQ=
AC•BC-
AP•QD=
(t-3)2+
,
∵
>0,
∴该抛物线的开口方向向上,该函数有最小值,
又∵0<t<5,
∴当t=3时,y最小=
.
即:当t=3时,y的值最小,其最小值为
;
(3)由题意得,若四边形AQPQ′是平行四边形,则四边形AQPQ′一定是菱形.
如答图3,连接QQ′交AP于点E,则QQ′⊥AP,且QQ′与AP互相平分.
∵由(2)得QE=QD=
(6-t),AE=
AP=t,且Rt△AEQ∽Rt△ACB,
∴
=
,即
=
,
解得 t=
.
 解:(1)当t=
解:(1)当t=| 30 |
| 11 |
| 18 |
| 13 |
∵如答图1,Rt△ABC中,AC=6cm,BC=8cm,
∴由勾股定理知 AB=
| AC2+BC2 |
由题意知,CQ=t,AQ=6-t,AP=2t.
若△APQ与△ABC相似时,分两种情况:△APQ∽△ABC或△APQ∽△ACB.
①当△APQ∽△ABC时,
| AP |
| AB |
| AQ |
| AC |
| 2t |
| 10 |
| 6-t |
| 6 |
解得 t=
| 30 |
| 11 |
②当△APQ∽△ACB时,
| AP |
| AC |
| AQ |
| AB |
| 2t |
| 6 |
| 6-t |
| 10 |
解得 t=
| 18 |
| 13 |

综上所述,当t=
| 30 |
| 11 |
| 18 |
| 13 |
(2)如答图2,过点Q作QD⊥AP,垂足为D.
∵∠A=∠A,AC⊥BC,
∴Rt△ADQ∽Rt△ACB,
∴
| AQ |
| AB |
| QD |
| BC |
∴QD=
| AQ•BC |
| AB |
| 4 |
| 5 |
由题意得:y=S△ABC-S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 84 |
| 5 |
∵
| 4 |
| 5 |
∴该抛物线的开口方向向上,该函数有最小值,
又∵0<t<5,
∴当t=3时,y最小=
| 84 |
| 5 |
即:当t=3时,y的值最小,其最小值为
| 84 |
| 5 |

(3)由题意得,若四边形AQPQ′是平行四边形,则四边形AQPQ′一定是菱形.
如答图3,连接QQ′交AP于点E,则QQ′⊥AP,且QQ′与AP互相平分.
∵由(2)得QE=QD=
| 4 |
| 5 |
| 1 |
| 2 |
∴
| AE |
| AC |
| QE |
| CB |
| t |
| 6 |
| ||
| 8 |
解得 t=
| 9 |
| 4 |
点评:本题考查了相似综合题.对于两个相似三角形,没有指出对应角(或对应边)时,一定要分类讨论.一般情况下,分三种情况进行讨论,不过在本题中,由于在△APQ与△ABC中,由一个公共角,所以分两种情况进行讨论:△APQ∽△ABC或△APQ∽△ACB;另外,在解答(2)时,通过配方法来求二次函数的最值的.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 如图:正方形ABCD的一条对角线AC的长为4cm,求它的边长和面积.(长度精确到0.1cm)
如图:正方形ABCD的一条对角线AC的长为4cm,求它的边长和面积.(长度精确到0.1cm) 如图,直线y=kx+b与双曲线y=
如图,直线y=kx+b与双曲线y=
 如图,在墙角O处有一个老鼠洞,小猫在A处发现自己的“冤家”老鼠正在B处准备往洞口方向逃窜,小猫想:“这一次不能再让你逃掉了.”于是立即前去捕捉,假设小猫与老鼠的速度相同,你能确定小猫抓住老鼠的位置吗?请在图中通过作图的方法标出(不需书写作图过程,保留作图痕迹即可).
如图,在墙角O处有一个老鼠洞,小猫在A处发现自己的“冤家”老鼠正在B处准备往洞口方向逃窜,小猫想:“这一次不能再让你逃掉了.”于是立即前去捕捉,假设小猫与老鼠的速度相同,你能确定小猫抓住老鼠的位置吗?请在图中通过作图的方法标出(不需书写作图过程,保留作图痕迹即可).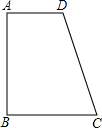 如图,已知AD∥BC,AB⊥BC,AD=2,BC=3,AB=4.
如图,已知AD∥BC,AB⊥BC,AD=2,BC=3,AB=4.