题目内容
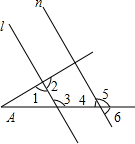 图中直线l、n分别截∠A的两边,且l∥n,∠3=∠1+∠4.根据图中标示的角,判断下列各角的度数关系中正确的是( )
图中直线l、n分别截∠A的两边,且l∥n,∠3=∠1+∠4.根据图中标示的角,判断下列各角的度数关系中正确的是( )| A、∠2+∠5>180° |
| B、∠2+∠3<180° |
| C、∠1+∠6>180° |
| D、∠3+∠4<180° |
考点:三角形内角和定理,平行线的性质,三角形的外角性质
专题:
分析:先根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠3,然后求出∠2+∠3,再根据两直线平行,同位角相等表示出∠2+∠5,根据邻补角的定义用∠5表示出∠6,再代入整理即可得到∠1+∠6,根据两直线平行,同旁内角互补表示出∠3+∠4,从而得解.
解答:解:根据三角形的外角性质,∠3=∠1+∠A,
∵∠1+∠2=180°,
∴∠2+∠3=∠2+∠1+∠A>180°,故B选项错误;
∵L∥N,
∴∠3=∠5,
∴∠2+∠5=∠2+∠1+∠A>180°,故A选项正确;
C、∵∠6=180°-∠5,
∴∠1+∠6=∠3-∠A+180°-∠5=180°-∠A<180°,故本选项错误;
D、∵L∥N,
∴∠3+∠4=180°,故本选项错误.
故选A.
∵∠1+∠2=180°,
∴∠2+∠3=∠2+∠1+∠A>180°,故B选项错误;
∵L∥N,
∴∠3=∠5,
∴∠2+∠5=∠2+∠1+∠A>180°,故A选项正确;
C、∵∠6=180°-∠5,
∴∠1+∠6=∠3-∠A+180°-∠5=180°-∠A<180°,故本选项错误;
D、∵L∥N,
∴∠3+∠4=180°,故本选项错误.
故选A.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图,在矩形ABCD中,有以下结论:
如图,在矩形ABCD中,有以下结论:①△AOB是等腰三角形;②S△ABO=S△ADO;③AC=BD;④AC⊥BD;⑤当∠ABD=45°时,矩形ABCD会变成正方形.
正确结论的个数是( )
| A、2 | B、3 | C、4 | D、5 |
下列命题中是真命题的是( )
| A、两直线被第三条直线所截,同位角相等 |
| B、掷一枚硬币200次,正面向上的频率必为0.5 |
| C、数据:3,5,7,9,11的极差是8 |
| D、三角形的外角大于三角形的内角 |
已知两个变量x和y,它们之间的3组对应值如下表,则y与x之间的函数关系式可能是( )
| x | -1 | 0 | 1 |
| y | -3 | -4 | -3 |
| A、y=3x | ||
| B、y=x-4 | ||
| C、y=x2-4 | ||
D、y=
|
 如图,四边形ABCD中,AD∥BC,∠B=60°,AB=AD=BO=4cm,OC=8cm,点M从B点出发,按从B→A→D→C的方向,沿四边形BADC的边以1cm/s的速度作匀速运动,运动到点C即停止.若运动的时间为t,△MOD的面积为y,则y关于t的函数图象大约是( )
如图,四边形ABCD中,AD∥BC,∠B=60°,AB=AD=BO=4cm,OC=8cm,点M从B点出发,按从B→A→D→C的方向,沿四边形BADC的边以1cm/s的速度作匀速运动,运动到点C即停止.若运动的时间为t,△MOD的面积为y,则y关于t的函数图象大约是( )



 如图,已知△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
如图,已知△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( ) 如图:正方形ABCD的一条对角线AC的长为4cm,求它的边长和面积.(长度精确到0.1cm)
如图:正方形ABCD的一条对角线AC的长为4cm,求它的边长和面积.(长度精确到0.1cm) 如图,直线y=kx+b与双曲线y=
如图,直线y=kx+b与双曲线y=