题目内容
公式ln(x1-x)2+(x2-x)2+…+(xn-x)2中,
(1)方差 ,数据个数 ,平均数 ,偏差 .(用字母表示)
(2)请你计算数据A:1,2,3,4,5的平均数、方差;
请你计算数据B:11,12,13,14,15平均数、方差;
请你计算数据C:10,20,30,40,50,平均数、方差.
(3)分别比较A、B、C的计算结果,你能发现什么规律?
(1)方差
(2)请你计算数据A:1,2,3,4,5的平均数、方差;
请你计算数据B:11,12,13,14,15平均数、方差;
请你计算数据C:10,20,30,40,50,平均数、方差.
(3)分别比较A、B、C的计算结果,你能发现什么规律?
考点:方差,算术平均数
专题:
分析:(1)分别用字母把方差、数据个数、平均数和偏差示出来即可;
(2)先计算出平均数,再根据方差公式进行计算即可;
(3)根据(2)得出的规律当一组数据的每个数据都加一个不为零的常数时,平均数也增加相同的数,方差不变;当一组数据的每个数据都扩大m倍时,这组数据的平均数也扩大m倍,但是方差扩大m2倍,即可得出答案.
(2)先计算出平均数,再根据方差公式进行计算即可;
(3)根据(2)得出的规律当一组数据的每个数据都加一个不为零的常数时,平均数也增加相同的数,方差不变;当一组数据的每个数据都扩大m倍时,这组数据的平均数也扩大m倍,但是方差扩大m2倍,即可得出答案.
解答:解:(1)方差s2,数据个数n,平均数
,偏差xn-
,
故答案为:s2,n,
,xn-
;
(2)计算数据A:平均数为(1+2+3+4+5)÷5=3,
方差为
[(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2]=2,
计算数据B:平均数为(11+12+13+14+15)÷5=13,
方差为
[(11-13)2+(12-13)2+(13-13)2+(14-13)2+(15-13)2]=2,
计算数据C:平均数为(10+20+30+40+50)÷5=30,
方差为
[(10-30)2+(20-30)2+(30-30)2+(40-30)2+(50-30)2]=200.
(3)比较A、B、C的计算结果,可得,当一组数据的每个数据都加一个不为零的常数时,平均数也增加相同的数,方差不变;当一组数据的每个数据都扩大m倍时,这组数据的平均数也扩大m倍,但是方差扩大m2倍.
. |
| x |
. |
| x |
故答案为:s2,n,
. |
| x |
. |
| x |
(2)计算数据A:平均数为(1+2+3+4+5)÷5=3,
方差为
| 1 |
| 5 |
计算数据B:平均数为(11+12+13+14+15)÷5=13,
方差为
| 1 |
| 5 |
计算数据C:平均数为(10+20+30+40+50)÷5=30,
方差为
| 1 |
| 5 |
(3)比较A、B、C的计算结果,可得,当一组数据的每个数据都加一个不为零的常数时,平均数也增加相同的数,方差不变;当一组数据的每个数据都扩大m倍时,这组数据的平均数也扩大m倍,但是方差扩大m2倍.
点评:此题考查了方差和算术平均数,一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 如图,已知△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
如图,已知△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )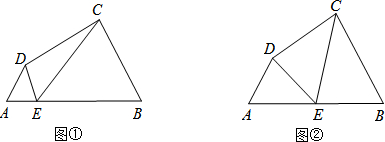

 如图,直线y=kx+b与双曲线y=
如图,直线y=kx+b与双曲线y=
 如图,在墙角O处有一个老鼠洞,小猫在A处发现自己的“冤家”老鼠正在B处准备往洞口方向逃窜,小猫想:“这一次不能再让你逃掉了.”于是立即前去捕捉,假设小猫与老鼠的速度相同,你能确定小猫抓住老鼠的位置吗?请在图中通过作图的方法标出(不需书写作图过程,保留作图痕迹即可).
如图,在墙角O处有一个老鼠洞,小猫在A处发现自己的“冤家”老鼠正在B处准备往洞口方向逃窜,小猫想:“这一次不能再让你逃掉了.”于是立即前去捕捉,假设小猫与老鼠的速度相同,你能确定小猫抓住老鼠的位置吗?请在图中通过作图的方法标出(不需书写作图过程,保留作图痕迹即可).