题目内容
 如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.
如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.(1)求证:△ABE≌△ADC;
(2)已知PE=2,AD=8,求PQ的长度.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据SAS即可证得△ABE≌△ADC;
(2)由)△ABE≌△ADC得出∠CAD=∠ABE,BE=AD=8,从而求得∠BPD=∠APE=∠BAC=60°进而得出∠PBQ=30°,在Rt△BPQ中,根据30°的直角三角形的性质即可求解.
(2)由)△ABE≌△ADC得出∠CAD=∠ABE,BE=AD=8,从而求得∠BPD=∠APE=∠BAC=60°进而得出∠PBQ=30°,在Rt△BPQ中,根据30°的直角三角形的性质即可求解.
解答:解:(1)∵CD=AE,∴BD=CE,
在△ABE和△ADC中,
,
∴△ABE≌△ADC(SAS);
(2)∵△ABE≌△ADC,
∴∠CAD=∠ABE,BE=AD=8,
∵∠APE=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°,
∴∠BPD=∠APE=∠BAC=60°,即∠BPD的度数为60°;
∵BQ⊥AD,
在Rt△BPQ中,∠BPQ=60°,
∴∠PBQ=30°,
∵PB=BE-PE=8-2=6,
∴PQ=
PB=3.
在△ABE和△ADC中,
|
∴△ABE≌△ADC(SAS);
(2)∵△ABE≌△ADC,
∴∠CAD=∠ABE,BE=AD=8,
∵∠APE=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°,
∴∠BPD=∠APE=∠BAC=60°,即∠BPD的度数为60°;
∵BQ⊥AD,
在Rt△BPQ中,∠BPQ=60°,
∴∠PBQ=30°,
∵PB=BE-PE=8-2=6,
∴PQ=
| 1 |
| 2 |
点评:本题考查了等边三角形各内角为60°的性质,考查了全等三角形的证明,考查了全等三角形对应角相等的性质,本题中求证∠APE=∠ABC是解题的关键.

练习册系列答案
相关题目
 如图所示下列说法正确的是( )
如图所示下列说法正确的是( )| A、点A在点O北偏东75°的方向上 |
| B、点A在点O北偏西75°的方向上 |
| C、点A在点O北偏东15°的方向上 |
| D、点A在点O北偏西15°的方向上 |
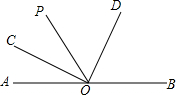 如图,OC、OD分别是∠AOP和∠POB的角平分线,那么∠COD=
如图,OC、OD分别是∠AOP和∠POB的角平分线,那么∠COD=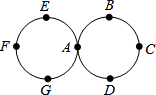 如图物体从点A出发,按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B→…的顺序循环运动,则第2015步到达点
如图物体从点A出发,按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B→…的顺序循环运动,则第2015步到达点 已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D.
已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D. 如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作
如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作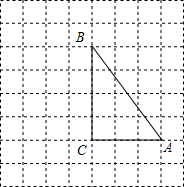 如图所示的网格中,每个小网格都是边长为1的正方形,每个小正方形的顶点叫格点,△ABC的顶点都在格点上.在AC的延长线上取一点D,D也在格点上,并连接BD.
如图所示的网格中,每个小网格都是边长为1的正方形,每个小正方形的顶点叫格点,△ABC的顶点都在格点上.在AC的延长线上取一点D,D也在格点上,并连接BD.