题目内容
 如图,在Rt△ACB中,∠ACB=90°,点D是AB上一点.将△BCD沿CD折叠,使B点落在AC边上的B′处.
如图,在Rt△ACB中,∠ACB=90°,点D是AB上一点.将△BCD沿CD折叠,使B点落在AC边上的B′处.(1)若∠A=28°,求∠ADB′的度数;
(2)若CD=CB,求∠ADB′的度数.
考点:翻折变换(折叠问题)
专题:
分析:(1)如图,求出∠CB′D=∠B=62°,根据∠A=28°,运用三角形外角的性质求出∠ADB′的度数,即可解决问题.
(2)求出∠DCB=45°;求出∠CDB=67.5°,即可解决问题.
(2)求出∠DCB=45°;求出∠CDB=67.5°,即可解决问题.
解答: 解:(1)∵∠A=28°,∠ACB=90°
解:(1)∵∠A=28°,∠ACB=90°
∴∠B=180°-∠A-∠ACB=62°;
∵△B′CD与△BCD关于CD对称(折叠性质)
∴∠CB′D=∠B=62°;
∵∠A+∠ADB′=∠CB′D,
∴∠ADB′=∠CB′D-∠A=62°-28°=34°.
(2)∵∠ACB=90°,且△B′CD与△BCD关于CD对称,
∴∠DCB=
∠ACB=45;
∵CD=CB,
∴∠CDB=
(180°-∠DCB)=67.5°,
∴∠ADB′=180°-2∠CDB=45°.
 解:(1)∵∠A=28°,∠ACB=90°
解:(1)∵∠A=28°,∠ACB=90°∴∠B=180°-∠A-∠ACB=62°;
∵△B′CD与△BCD关于CD对称(折叠性质)
∴∠CB′D=∠B=62°;
∵∠A+∠ADB′=∠CB′D,
∴∠ADB′=∠CB′D-∠A=62°-28°=34°.
(2)∵∠ACB=90°,且△B′CD与△BCD关于CD对称,
∴∠DCB=
| 1 |
| 2 |
∵CD=CB,
∴∠CDB=
| 1 |
| 2 |
∴∠ADB′=180°-2∠CDB=45°.
点评:该题主要考查了翻折变换的性质、直角三角形的性质等几何知识点及其应用问题;解题的关键是牢固掌握翻折变换的性质、直角三角形的性质等几何知识点,这是灵活运用的基础.

练习册系列答案
相关题目
若抛物线y=x2-4x+3-t(t为实数)在0<x<3
的范围内与x轴有公共点,则t的取值范围为( )
| 1 |
| 2 |
| A、-1<t<3 | ||
| B、-1≤t<3 | ||
C、
| ||
| D、t≥-1 |
 如图所示下列说法正确的是( )
如图所示下列说法正确的是( )| A、点A在点O北偏东75°的方向上 |
| B、点A在点O北偏西75°的方向上 |
| C、点A在点O北偏东15°的方向上 |
| D、点A在点O北偏西15°的方向上 |
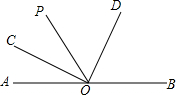 如图,OC、OD分别是∠AOP和∠POB的角平分线,那么∠COD=
如图,OC、OD分别是∠AOP和∠POB的角平分线,那么∠COD=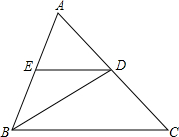 如图,在△ABC中,∠AED=80°,BD是∠ABC的平分线,∠DBC=40°,求∠EDB的度数.
如图,在△ABC中,∠AED=80°,BD是∠ABC的平分线,∠DBC=40°,求∠EDB的度数.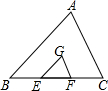 如图,点G是△ABC的重心,过G作CG∥AB,交BC于点E,GF∥AC,交AB于点F,则S△GEF:S△ABC=
如图,点G是△ABC的重心,过G作CG∥AB,交BC于点E,GF∥AC,交AB于点F,则S△GEF:S△ABC= 如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作
如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作