题目内容
13.设k≥2,解关于x的方程x3+2kx2+(k2+1)x+k=0.分析 将方程的左边分解因式为:(x+k)(x2+kx+1)=0,解出方程即可;注意当x2+kx+1=0时,先计算△的值,利用已知的k≥2,确定△≥0,解方程.
解答 解:x3+2kx2+(k2+1)x+k=0,
x3+2kx2+k2x+x+k=0,
x(x2+2kx+k2)+(x+k)=0,
x(x+k)2+(x+k)=0,
(x+k)[x(x+k)+1]=0,
(x+k)(x2+kx+1)=0,
x+k=0或x2+kx+1=0,
∴x1=-k,
x2+kx+1=0,
△=k2-4,
∵k≥2,
∴△≥0,
∴x=$\frac{-k±\sqrt{{k}^{2}-4}}{2}$,
综上所述,原方程的解为:x1=-k,x2=$\frac{-k+\sqrt{{k}^{2}-4}}{2}$,x3=$\frac{-k-\sqrt{{k}^{2}-4}}{2}$.
点评 本题是解高次方程,此类题都要对方程进行变形:因式分解或利用换元法;达到降次的目的,从而求出方程的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.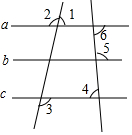 如图,下列命题是假命题的是( )
如图,下列命题是假命题的是( )
 如图,下列命题是假命题的是( )
如图,下列命题是假命题的是( )| A. | 如果∠2=∠3,那么a∥c | B. | 如果a∥b,a∥c,那么b∥c | ||
| C. | 如果∠4+∠5=180°,那么∠2=∠3 | D. | 如果∠4=∠6,那么∠1+∠3=180° |
8.某水果店有甲、乙两种苹果包装盒,现有360个苹果要用这两种包装盒进行包装,已知每个甲包装盒比每个乙
包装盒少装3个苹果,单独用甲包装盒比单独用乙包装盒多用6个,设每个甲包装盒可装x个苹果,根据题意
下面所列方程正确的是( )
包装盒少装3个苹果,单独用甲包装盒比单独用乙包装盒多用6个,设每个甲包装盒可装x个苹果,根据题意
下面所列方程正确的是( )
| A. | $\frac{360}{x}$=$\frac{360}{x-3}$+6 | B. | $\frac{360}{x}$=$\frac{360}{x+3}$+6 | C. | $\frac{360}{x-3}$=$\frac{360}{x}$+6 | D. | $\frac{360}{x+3}$=$\frac{360}{x}$+6 |
3. 实数a在数轴上对应点的位置如图,则a,-a,1的大小关系是( )
实数a在数轴上对应点的位置如图,则a,-a,1的大小关系是( )
 实数a在数轴上对应点的位置如图,则a,-a,1的大小关系是( )
实数a在数轴上对应点的位置如图,则a,-a,1的大小关系是( )| A. | -a<a<1 | B. | 1<-a<a | C. | a<1<-a | D. | a<-a<1 |
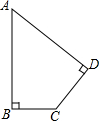 如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=2m,CD=1m.求这块草地的面积和周长.
如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=2m,CD=1m.求这块草地的面积和周长.
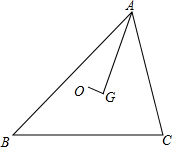 点O、G分别是△ABC的外心和重心,若AG⊥OG,求$\frac{A{B}^{2}+A{C}^{2}}{B{C}^{2}}$的值.
点O、G分别是△ABC的外心和重心,若AG⊥OG,求$\frac{A{B}^{2}+A{C}^{2}}{B{C}^{2}}$的值.
 如图,长为10cm的弹性皮筋直放置在直线l上,固定两端A和B,然后把中点C垂直向上拉升12cm至D点,则弹性皮筋被拉长了16cm.
如图,长为10cm的弹性皮筋直放置在直线l上,固定两端A和B,然后把中点C垂直向上拉升12cm至D点,则弹性皮筋被拉长了16cm.