题目内容
4.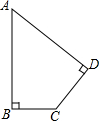 如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=2m,CD=1m.求这块草地的面积和周长.
如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=2m,CD=1m.求这块草地的面积和周长.
分析 分别延长AD,BC交于点E,所求四边形ABCD的面积=S△ABE-S△CED.由∠A=45°,∠B=∠D=90°,可得△ABE和△CDE都是等腰直角三角形,然后求出△ABE和△CDE的面积即可求解.
解答 解:分别延长AD,BC交于点E.如图所示,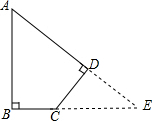
∵∠A=45°,∠B=∠D=90°,
∴∠DCE=∠DEB=∠A=45°,
∴AB=BE,CD=DE,
∵AB=2m,CD=1m,
∴BE=2m,DE=1m,
∴BC=BE-CE=2-$\sqrt{2}$,AD=AE-DE=2$\sqrt{2}$-1,
∵S△ABE=$\frac{1}{2}$AB•BE=2,S△CDE=$\frac{1}{2}$CD•DE=0.5,
∴四边形ABCD的面积=S△ABE-S△CDE=2-0.5=1.5(m2).
四边形ABCD的周长=AB+BC+CD+AD=2+2-$\sqrt{2}$+1+2$\sqrt{2}$-1=4+$\sqrt{2}$(m)
所以这块草地的面积为1.5m2.周长为(4+$\sqrt{2}$)m.
点评 本题考查了等腰直角三角形的性质,勾股定理的应用.解题的关键是:通过作辅助线,构造新的直角三角形,利用四边形ABCD的面积=S△ABE-S△CED来求解.

练习册系列答案
相关题目
16.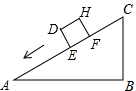 一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.
一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.
 一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.
一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.| A. | $\frac{16}{3}$ | B. | $\frac{14}{3}$ | C. | 5 | D. | 4 |
14. 如图,已知四边形ABCD是正方形,P是直线AD上一动点,使△PBC是等腰三角形的点P有( )
如图,已知四边形ABCD是正方形,P是直线AD上一动点,使△PBC是等腰三角形的点P有( )
 如图,已知四边形ABCD是正方形,P是直线AD上一动点,使△PBC是等腰三角形的点P有( )
如图,已知四边形ABCD是正方形,P是直线AD上一动点,使△PBC是等腰三角形的点P有( )| A. | 1个 | B. | 3个 | C. | 5个 | D. | 7个 |
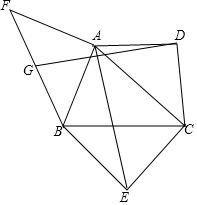 如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明.
如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明.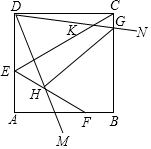 正方形ABCD中,AB=4,点E为AD边上一点,点F为AB边上一点且∠DEC=∠AEF=60°,将顶点为D点的∠NDM绕着D点进行旋转,∠NDM=60°,若射线DM交线段EF于点H,若射线DN交线段EC于K点,交线段CB于G点,当HG平分∠DHF时,四边形EHGK的面积是$\frac{29}{15}\sqrt{3}$.
正方形ABCD中,AB=4,点E为AD边上一点,点F为AB边上一点且∠DEC=∠AEF=60°,将顶点为D点的∠NDM绕着D点进行旋转,∠NDM=60°,若射线DM交线段EF于点H,若射线DN交线段EC于K点,交线段CB于G点,当HG平分∠DHF时,四边形EHGK的面积是$\frac{29}{15}\sqrt{3}$.