题目内容
10.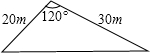 某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )| A. | $450\sqrt{3}a$元 | B. | $225\sqrt{3}a$元 | C. | $150\sqrt{3}a$元 | D. | $300\sqrt{3}a$ |
分析 求三角形的面积,作出高线,根据三角函数求得高线的长,利用面积公式即可求解.
解答  解:如图,作BD⊥AC于点D,
解:如图,作BD⊥AC于点D,
在直角△ADB中,BD=AB•sin60°=10$\sqrt{3}$,
则△ABC的面积是$\frac{1}{2}$•AC•BD=$\frac{1}{2}$×30×10$\sqrt{3}$=150$\sqrt{3}$.
因而购买这种草皮至少需要150$\sqrt{3}$a元.
故选C.
点评 此题是解直角三角形的应用,主要考查了三角形的面积的计算方法,锐角三角函数,同时在解题中注意解三角形的条件.

练习册系列答案
相关题目
20.在-6,9.3,-2π,3.3030030003…,$\frac{22}{7}$这5个数中,无理数有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
 如图,在△ABC中,添加一个条件:∠ABP=∠C或∠APB=∠ABC或AB2=AP•AC,使△ABP∽△ACB.
如图,在△ABC中,添加一个条件:∠ABP=∠C或∠APB=∠ABC或AB2=AP•AC,使△ABP∽△ACB.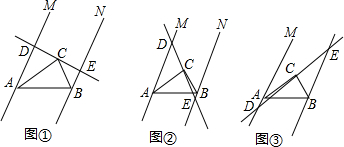
 如图,AD、BE、CF是⊙O的直径,且∠AOF=∠BOC=∠DOE.求证:AB=CD=EF.
如图,AD、BE、CF是⊙O的直径,且∠AOF=∠BOC=∠DOE.求证:AB=CD=EF. 已知,如图,△ABC中,AB=AC,AE=CD,BE交AD于点P,∠BAC=∠C=60°,
已知,如图,△ABC中,AB=AC,AE=CD,BE交AD于点P,∠BAC=∠C=60°, 如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.