题目内容
16.学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人.已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
分析 (1)可设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,根据等量关系:①1辆甲种客车和3辆乙种客车共需租金1240元,②3辆甲种客车和2辆乙种客车共需租金1760元,列出方程组求解即可;
(2)由于求最节省的租车费用,可知租用甲种客车6辆,租用乙客车2辆,进而求解即可.
解答 解:(1)设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,依题意有
$\left\{\begin{array}{l}{x+3y=1240}\\{3x+2y=1760}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=400}\\{y=280}\end{array}\right.$.
故1辆甲种客车的租金是400元,1辆乙种客车的租金是280元;
(2)方法1:租用甲种客车6辆,租用乙客车2辆是最节省的租车费用,
400×6+280×2
=2400+560
=2960(元).
方法2:设租用甲种客车x辆,依题意有
45x+30(8-x)≥330,
解得x≥6,
租用甲种客车6辆,租用乙客车2辆的租车费用为:
400×6+280×2
=2400+560
=2960(元);
租用甲种客车7辆,租用乙客车1辆的租车费用为:
400×7+280
=2800+280
=3080(元);
2960≤3080,
故最节省的租车费用是2960元.
点评 本题考查一元一次不等式及二元一次方程组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系.

练习册系列答案
相关题目


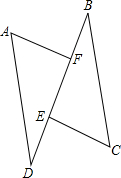 已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,垂足分别为F、E,连接AD、BC,AD=CB,DE=BF,求证:AF=CE.
已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,垂足分别为F、E,连接AD、BC,AD=CB,DE=BF,求证:AF=CE.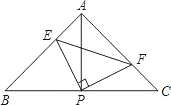 已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下结论:
已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下结论: